![[Shownotes]](../gif/annotate/shide-81.gif)
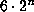 -gons about a circle of diameter 1. Call these quantities
-gons about a circle of diameter 1. Call these quantities 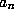 and
and 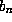 .
respectively. Then
.
respectively. Then 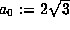 ,
, 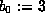 and, as Gauss's teacher Pfaff
discovered in 1800,
and, as Gauss's teacher Pfaff
discovered in 1800,

 Archimedes, with n=4, obtained
Archimedes, with n=4, obtained

 While hardly better than estimates one could get with a ruler, this is the first
method that can be used to generate an arbitrary number of digits, and to a
nonnumerical mathematician perhaps the problem ends here. Variations on this theme
provided the basis for virtually all calculations of
While hardly better than estimates one could get with a ruler, this is the first
method that can be used to generate an arbitrary number of digits, and to a
nonnumerical mathematician perhaps the problem ends here. Variations on this theme
provided the basis for virtually all calculations of  for the next 1800 years,
culminating with a 34 digit calculation due to Ludolph van Ceulen (1540--1610). This
demands polygons with about
for the next 1800 years,
culminating with a 34 digit calculation due to Ludolph van Ceulen (1540--1610). This
demands polygons with about 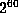 sides and so is extraordinarily time consuming.
sides and so is extraordinarily time consuming.