The purpose of this paper is to present some results and observations regarding the
beta transformations introduced by Rényi [8]. Given 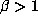 , the
beta transformation
, the
beta transformation 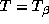 is defined for
is defined for 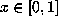 by
by 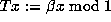 . Parry [7] defined
. Parry [7] defined 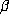 to be a beta number if the orbit
to be a beta number if the orbit
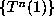 is finite. If
is finite. If 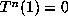 for some n, then
for some n, then 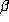 is a simple
beta number. If
is a simple
beta number. If 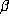 is a beta number which is not simple, then there is some
smallest
is a beta number which is not simple, then there is some
smallest 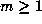 (the preperiod length) and
(the preperiod length) and 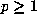 (the period
length) for which
(the period
length) for which 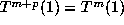 . For a simple beta number we define m = 0
and p to be the smallest integer with
. For a simple beta number we define m = 0
and p to be the smallest integer with 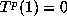 . Notice that m+p is the size
of the orbit
. Notice that m+p is the size
of the orbit 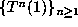 .
.
 Annotation Form Interface
Annotation Form Interface
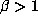 , the
beta transformation
, the
beta transformation 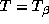 is defined for
is defined for 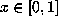 by
by 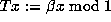 . Parry [7] defined
. Parry [7] defined 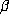 to be a beta number if the orbit
to be a beta number if the orbit
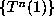 is finite. If
is finite. If 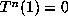 for some n, then
for some n, then 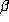 is a simple
beta number. If
is a simple
beta number. If 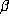 is a beta number which is not simple, then there is some
smallest
is a beta number which is not simple, then there is some
smallest 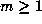 (the preperiod length) and
(the preperiod length) and 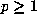 (the period
length) for which
(the period
length) for which 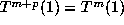 . For a simple beta number we define m = 0
and p to be the smallest integer with
. For a simple beta number we define m = 0
and p to be the smallest integer with 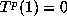 . Notice that m+p is the size
of the orbit
. Notice that m+p is the size
of the orbit 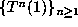 .
.