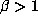, the
beta transformation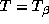 
is defined for 
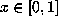by 
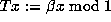. Parry [7] defined 
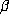to be a beta number if the orbit
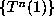is finite. If 
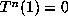for some n, then 
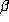is a simple
beta number. If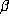 
is a beta number which is not simple, then there is some
smallest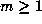 
(the preperiod length) and 
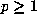(the period
length) for which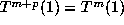 
. For a simple beta number we define m = 0
and p to be the smallest integer with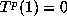 
. Notice that m+p is the size
of the orbit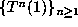 
.
It is easy to see by induction (see below) that there are integers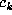 
with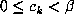 
(the digits in the beta expansion of 1) for
which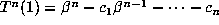 
, so that 
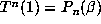, where
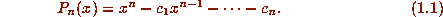Thus, if 
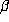is a beta number, then 
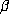satisfies the polynomial equation
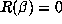, where
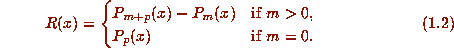In particular, a beta number is an algebraic integer whose minimal polynomial 
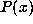divides 
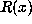. The degree 
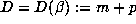of R is the beta degree of
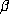, which is in general larger than 
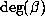, the degree of 
,
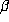which is defined to be the degree of its minimal polynomial P. As we observed above,
D is the size of the orbit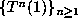 
.
The polynomial R is called the characteristic polynomial of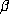 
. Parry
[7] showed that the roots of R other than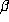 
lie in the disk 
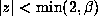. This was improved to 
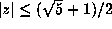by Solomyak [11]
and Flatto, Lagarias and Poonen [4] independently. In fact, Solomyak gives an
exact description of the compact subset of the plane which is the closure of the set of
all conjugates (other than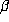 
) of beta numbers.
Recall that a Pisot number (or Pisot-Vijayaraghavan number, or PV
number) is an algebraic integer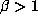 
for which all conjugates 
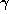of
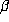with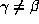 
satisfy 
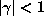. A Salem number is an
algebraic integer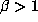 
for which all conjugates 
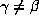satisfy
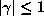with at least one conjugate having 
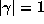. This implies that
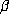is reciprocal, so 
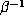is a conjugate of 
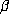and all other conjugates
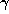satisfy 
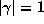. Hence, 
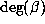is even and 
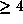[9], p.26.
Schmidt [10] showed that every Pisot number is a beta number. This was also proved
independently by Bertrand [1]. The idea behind the proof, which is based on the
box principle, goes back to a paper of Gelfond [5]. Schmidt also showed that if
every rational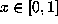 
has a periodic expansion in base 
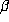(i.e., the orbit
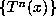is finite), then 
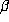must be a Pisot or Salem number. He conjectured
that the converse is true, so in particular that every Salem number would be a beta
number. A simple result from [3] is that a Salem number cannot be a
simple beta number: clearly the characteristic polynomial of a simple beta number
has a unique positive root, but a Salem number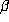 
has two positive conjugates,
namely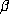 
and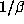 
.
In [3], we showed that if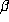 
is a Salem number of degree 4, then 
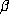is a
beta number. (We did not consider Schmidt's more general conjecture there; it remains
open for Salem numbers of all degrees). The explicit beta expansion of each such
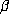was given. In all cases m = 1, i.e., 
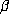(mod 1) is a purely periodic
point of T. If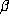 
has the minimal polynomial 
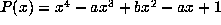, then for fixed a the period 
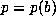is a unimodal function of b and takes
on values which lie in the set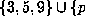 
even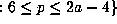 
.
Thus,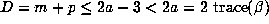 
for all Salem numbers of degree
4. No such bound seems to be true for Salem numbers of higher degree.
If we write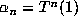 
, then the canonical beta expansion of 1 to base
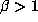is defined by the ``greedy'' algorithm: 
, 
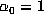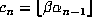and 
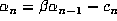, for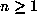 
.
Clearly,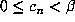 
for all n, and
We will refer to the sequence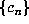 
as the beta expansion (of 1) for 
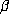. If
this expansion is periodic, with preperiod length m and period length p, we denote
it by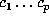 
, if m = 0, and by 
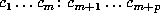if
m > 0. A simple criterion for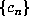 
to be the
beta expansion for some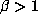 
was given by Parry [7],p.407:
the sequence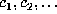 
must dominate, in the sense of lexicographic order, the
shifted sequences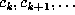 
, for all 
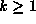. The number 
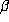is then
determined by (1.3). For periodic expansions,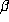 
is also determined by (1.2).
Our main purpose here is to consider whether Salem numbers of degree 6 must be beta
numbers. We compute the beta expansions for all but 80 of the
Salem numbers of degree 6 and trace at most 15 (there are 11836 such numbers).
For all but 199 of these, we have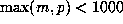 
. However, there is one example
for which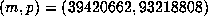 
, and two examples for which we can show
that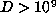 
but do not know whether 
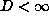. The
existence of such examples shows that the situation for Salem numbers of degree 6 is
certainly more complicated than the degree-4 case. However, the fact that there
are examples with D very large but finite perhaps supports Schmidt's
conjecture for Salem numbers of degree 6.
In § 6, we give a heuristic probabilistic argument based on ideas of the geometry of
numbers which makes plausible the observed difference between the cases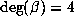 
and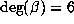 
. The argument correctly predicts that 
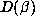will be
small relative to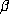 
for Salem numbers of degree 4. It predicts that almost all
Salem numbers of degree 6 will be beta numbers but that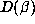 
can be arbitrarily
large even for small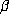 
. Moreover, it predicts that for each fixed even degree 
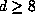there should be a positive proportion of Salem numbers of degree d which
are not beta numbers, as well as a positive proportion that are beta numbers. We
present no computational evidence here for this latter prediction.
The heuristic argument suggests, for Salem numbers of fixed degree d, that the size of
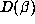is directly related to the size of 
. Here
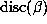denotes the discriminant of the polynomial P. We explore this
connection through some of the computed examples for d = 6.
The heuristic arguments
apply equally well to Schmidt's more general conjecture concerning the periodicity of
the beta expansions of rationals to a Salem number base, and predict that Schmidt's
conjecture is true for numbers of degree 4 or 6 and false for numbers of higher
degree. For d = 4, the model predicts that the size of the orbit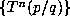 
for
fixed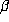 
should be roughly proportional to 
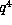. These predictions are not
tested here.
![[Annotate]](/organics/icons/sannotate.gif){kind=icon}
![[Shownotes]](../gif/annotate/shide-11.gif)