

Contents
Next: About this document
Up: No Title
Previous: The expected size
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-161.gif)
References
- 1
-
A. Bertrand,
Développements en base de Pisot et répartition modulo 1,
C.R. Acad. Sci. Paris Sér. I Math.,
vol 285 1977 pages 419--421
[1] [2]
- 2
-
Z.I. Borevich and I.R. Shafarevich,
Number Theory,
Academic Press New York and London,
1966
[1] [2]
- 3
-
D.W. Boyd,
Salem numbers of degree four have periodic expansions,
Théorie des Nombres -- Number Theory,
J.M. de Koninck and C. Levesque,
Walter de Gruyter & Co. Berlin and New York ,
1989 pages 57--64
[1] [2] [3] [4]
- 4
-
L. Flatto, J.C. Lagarias and B. Poonen,
The zeta function of the beta transformation,
Ergodic Theory Dynamical Systems,
vol 14 1994 237--266
[1]
- 5
-
A.O. Gelfond,
On a general property of number systems,
Russian,
Izv. Akad. Nauk SSSR Ser. Mat. ,
vol 23 1959 pages 809--814
[1]
- 6
-
D. Knuth,
The Art of Computer Programming, volume 1: Fundamental Algorithms,
Addison-Wesley Massachusetts,
1968
[1]
- 7
-
W. Parry,
On the
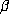 -expansions of real numbers,
Acta Math. Hungar. ,
vol 11 1960 pages 401--416
-expansions of real numbers,
Acta Math. Hungar. ,
vol 11 1960 pages 401--416
[1] [2] [3] [4] [5]
- 8
-
A. Rényi,
Representations for real numbers and their ergodic properties,
Acta Math. Hungar.,
vol 8 1957 pages 477-493
[1]
- 9
-
R. Salem,
Algebraic numbers and Fourier analysis,
D. C. Heath & Co. Boston,
1963
[1]
- 10
-
K. Schmidt,
On periodic expansions of Pisot numbers and Salem numbers,
Bull. London Math. Soc. ,
vol 12 1980 pages 269--278
[1]
- 11
-
B. Solomyak,
Conjugates of beta-numbers and the zero-free domain for a
class of analytic functions,
Proc. London Math. Soc. (3),
vol 68 1994 pages 477--498
[1]


Contents
Next: About this document
Up: No Title
Previous: The expected size
![[Shownotes]](../gif/annotate/sshow-161.gif)
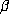 -expansions of real numbers,
Acta Math. Hungar. ,
vol 11 1960 pages 401--416
-expansions of real numbers,
Acta Math. Hungar. ,
vol 11 1960 pages 401--416