![[Shownotes]](../gif/annotate/shide-151.gif)
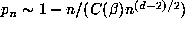 be the probability that
be the probability that 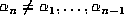 . Then the probability that the points
. Then the probability that the points
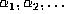 are distinct is
are distinct is

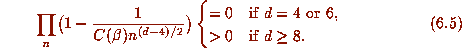
This suggests that almost all orbits are finite if n = 4,6 while a positive
proportion are infinite if 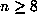 .
.
We can distinguish the cases n = 4 and n = 6 by considering the expected
size (D = m+p) of the orbit. Using the familiar fact that 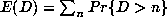 , we compute
, we compute

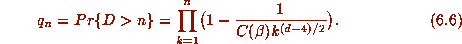 For d =4, we thus have
For d =4, we thus have 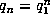 , so
, so

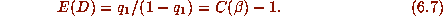 On the other hand, if d = 6, then
On the other hand, if d = 6, then

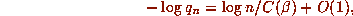 i.e.,
i.e., 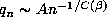 , so that
, so that

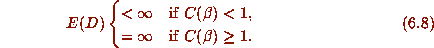
Remark 6.2 For d = 4, we have shown rigorously in [3] that
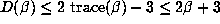 . The largest value of
. The largest value of 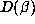 for
for
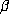 with a fixed value of
with a fixed value of 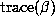 is attained by the
is attained by the 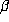 with minimal
polynomial
with minimal
polynomial 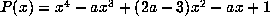 . By (2.4), P has discriminant
. By (2.4), P has discriminant
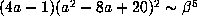 for large
for large 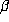 , so that from (6.4),
, so that from (6.4),
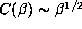 . Thus (6.7) predicts a smaller value for
. Thus (6.7) predicts a smaller value for 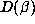 than
actually attained but it does predict that large values of
than
actually attained but it does predict that large values of 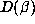 occur for small
values of
occur for small
values of 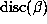 and vice versa.
and vice versa.
Remark 6.3 For d = 6, the data tends to confirm a direct relationship
between the sizes of 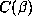 and
and 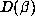 , although not quite as dramatic as (6.8)
would suggest. There are some exceptions as well: for example if
, although not quite as dramatic as (6.8)
would suggest. There are some exceptions as well: for example if 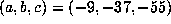 , then
, then 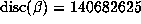 is quite small, so
is quite small, so 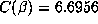 is
large, but
is
large, but 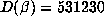 is not exceptionally large. On the other hand, the
example
is not exceptionally large. On the other hand, the
example 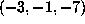 with
with 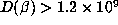 only has
only has 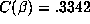 , which
is not very large (although it is the largest value of
, which
is not very large (although it is the largest value of 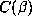 by far in
Table 3, i.e., for
by far in
Table 3, i.e., for 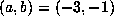 ). This is perhaps to be expected, given the number
of unsupported assumptions we have had to make to arrive at (6.8).
). This is perhaps to be expected, given the number
of unsupported assumptions we have had to make to arrive at (6.8).
Perhaps the most questionable argument is the deduction of the exponent 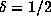 in .4. Let
in .4. Let 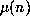 denote the maximum modulus of the conjugates of
denote the maximum modulus of the conjugates of 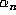 ,
i.e., the largest modulus of the eigenvalues of the matrix
,
i.e., the largest modulus of the eigenvalues of the matrix 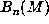 discussed in .2.
A fit of a power curve to data from the first 20000 values of
discussed in .2.
A fit of a power curve to data from the first 20000 values of 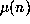 for the case
for the case
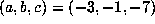 suggests an exponent
suggests an exponent 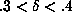 for this example. A
plot of
for this example. A
plot of 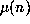 versus n in this range suggests some sort of random process but
perhaps not one well described by the model of .4. Note that, for d = 6, we only
need
versus n in this range suggests some sort of random process but
perhaps not one well described by the model of .4. Note that, for d = 6, we only
need 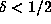 to apply the birthday paradox argument of .3, so if the growth
observed for
to apply the birthday paradox argument of .3, so if the growth
observed for 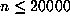 were to persist, then .3 would predict a periodic beta
expansion for this
were to persist, then .3 would predict a periodic beta
expansion for this 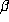 .
.
To test this, let us consider the behavior of the record values of 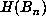 for large
n still for this
for large
n still for this 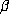 . So, let
. So, let 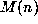 denote the largest value of
denote the largest value of 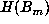 for
for 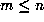 . For
. For 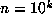 ,
, 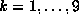 , we find that
, we find that

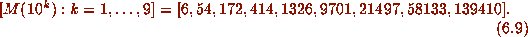 Fitting a power curve to these 9 values (by a linear least squares fit to their
logarithms) gives a curve
Fitting a power curve to these 9 values (by a linear least squares fit to their
logarithms) gives a curve 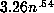 , suggesting
, suggesting 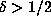 . On the other
hand, using only
. On the other
hand, using only 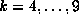 gives
gives 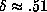 , while the data for
the 5 values
, while the data for
the 5 values 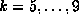 is very well fitted by a curve with
is very well fitted by a curve with 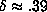 . Apparently, this data does not exclude or confirm a growth rate of
. Apparently, this data does not exclude or confirm a growth rate of 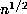 .
Another instructive example is
.
Another instructive example is 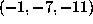 , where
, where 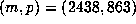 .
Here,
.
Here, 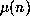 is quite well fitted for
is quite well fitted for 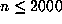 by a curve
by a curve 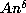 with
with 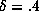 . Of course, this cannot hold for
. Of course, this cannot hold for  since
since 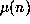 is ultimately
periodic.
is ultimately
periodic.
Remark 6.4 Our computations have concentrated on the question of whether
Salem numbers are beta numbers and not on Schmidt's more general conjecture that, for
every Salem number 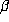 and every rational
and every rational 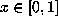 , the orbit
, the orbit 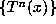 should be finite. Our heuristic arguments apply equally well to this conjecture. If
should be finite. Our heuristic arguments apply equally well to this conjecture. If 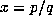 , then the iterates
, then the iterates 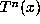 lie in
lie in 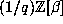 , and hence we need only
replace the lattice
, and hence we need only
replace the lattice 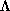 by
by 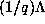 in the arguments of .1 to .6. The
only change is that the density of the points of
in the arguments of .1 to .6. The
only change is that the density of the points of 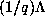 in
in 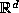 is
is 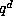 times as large as the density of the points of
times as large as the density of the points of 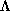 . Thus, the qualitative
predictions of .1 to .4 are unchanged, i.e., we predict that Schmidt's conjecture
is true for Salem numbers of degree 4 and 6 but not for higher degrees. The main
change in the more quantitative analysis of .5 and .6 is that
. Thus, the qualitative
predictions of .1 to .4 are unchanged, i.e., we predict that Schmidt's conjecture
is true for Salem numbers of degree 4 and 6 but not for higher degrees. The main
change in the more quantitative analysis of .5 and .6 is that 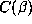 must be
replaced by
must be
replaced by 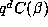 . Thus, .6 would suggest that, for fixed
. Thus, .6 would suggest that, for fixed 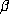 , the size
of the orbit
, the size
of the orbit 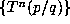 should increase with q as predicted by (6.7) and (6.8).
That is, for d = 4 the size of the orbit should be roughly proportional to
should increase with q as predicted by (6.7) and (6.8).
That is, for d = 4 the size of the orbit should be roughly proportional to 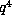 , and
for d = 6 we should expect unusually large orbits as soon as
, and
for d = 6 we should expect unusually large orbits as soon as 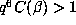 .
It would be interesting to test these predictions by further computation.
.
It would be interesting to test these predictions by further computation.