![[Shownotes]](../gif/annotate/shide-71.gif)
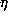 at each step, is to
compute
at each step, is to
compute 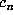 by using integer arithmetic. Let M be the companion matrix to
by using integer arithmetic. Let M be the companion matrix to 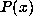 , so
that the eigenvalues of M are the conjugates of
, so
that the eigenvalues of M are the conjugates of 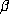 . If
. If 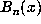 , as above, is
such that
, as above, is
such that 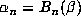 , then the eigenvalues of
, then the eigenvalues of 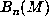 are the conjugates
of
are the conjugates
of 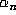 and the eigenvalues of
and the eigenvalues of 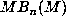 are the conjugates of
are the conjugates of 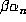 .
.
Now, 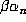 has exactly two real conjugates corresponding to the two
conjugates
has exactly two real conjugates corresponding to the two
conjugates 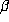 and
and 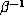 of
of 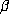 . Since
. Since 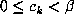 for all k,
it is easy to see that the conjugate of
for all k,
it is easy to see that the conjugate of 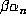 corresponding to
corresponding to 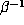 is
is 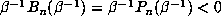 . Let us denote this
conjugate by
. Let us denote this
conjugate by 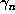 . For
. For 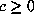 ,
, 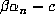 has two real
conjugates
has two real
conjugates 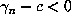 and
and 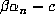 itself. By definition,
itself. By definition, 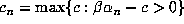 . Since all other conjugates are nonreal, the sign of
the product of all conjugates is determined by that of
. Since all other conjugates are nonreal, the sign of
the product of all conjugates is determined by that of 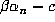 , and thus
, and thus

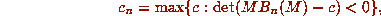 which is a compuation involving only
finding the determinant of a finite number of matrices with integer entries.
Note that the matrix
which is a compuation involving only
finding the determinant of a finite number of matrices with integer entries.
Note that the matrix 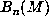 is as good a representation of
is as good a representation of 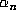 as is
as is 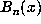 and can be computed from the recursion
and can be computed from the recursion 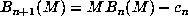 without explicitly
computing the coefficients of
without explicitly
computing the coefficients of 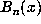 . Of course,
. Of course, 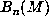 has
has 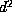 integer entries
rather than the d entries of the coefficient vector of
integer entries
rather than the d entries of the coefficient vector of 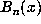 .
.
Since the determinant computed above is just the resultant of 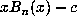 and
and 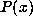 ,
another alternative is to use the coefficient vector of
,
another alternative is to use the coefficient vector of 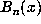 to represent
to represent
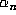 and replace the determinant computation by the computation of a resultant at
each step. Or, combining the approaches of § 5.1 and § 5.2, one could compute
and replace the determinant computation by the computation of a resultant at
each step. Or, combining the approaches of § 5.1 and § 5.2, one could compute 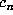 using floating point except in ``delicate'' cases.
Experiments showed that the approach of § 5.2 was generally considerably slower than
that of § 5.1.
using floating point except in ``delicate'' cases.
Experiments showed that the approach of § 5.2 was generally considerably slower than
that of § 5.1.