![[Shownotes]](../gif/annotate/sshow-81.gif)
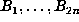 ,
one tests whether
,
one tests whether 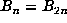 . If
. If 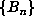 is periodic with
is periodic with 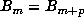 for
minimal m and p, and if n = sp satisfies
for
minimal m and p, and if n = sp satisfies 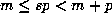 , then
, then 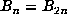 .
Once n = sp is found, one determines p by finding the minimal divisor of n for
which
.
Once n = sp is found, one determines p by finding the minimal divisor of n for
which 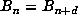 . Finally, one finds m by testing whether
. Finally, one finds m by testing whether 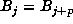 for
for
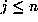 .
.
For small N, one can do this in a straightforward way for 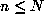 by storing a
table of
by storing a
table of 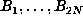 . For larger N, once memory becomes insufficient, one
instead computes
. For larger N, once memory becomes insufficient, one
instead computes 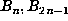 and
and 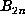 at each step. This requires 3N of the
basic steps to reach n = N, rather than 2N.
at each step. This requires 3N of the
basic steps to reach n = N, rather than 2N.
If we have not proved that the sequence is periodic by the time we have reached
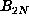 , then we know that D = m+p > N. This observation accounts for only one
of the lower bounds in
Table 2
, namely
, then we know that D = m+p > N. This observation accounts for only one
of the lower bounds in
Table 2
, namely 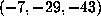 , for which the lower bound is
exactly
, for which the lower bound is
exactly 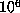 .
.
A more useful method for obtaining lower bounds on m+p is based on the following
observation. Let 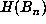 denote the maximum of the absolute values of the coefficients
of
denote the maximum of the absolute values of the coefficients
of 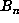 . During the computation, maintain a list of the record values of
. During the computation, maintain a list of the record values of 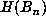 ,
i.e., those n for which
,
i.e., those n for which 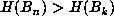 for all k < n. Clearly, if
for all k < n. Clearly, if 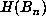 is
a record, then
is
a record, then 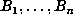 are all distinct, so we know that D > n. In those
cases for which a preliminary computation up to
are all distinct, so we know that D > n. In those
cases for which a preliminary computation up to 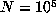 , say, had indicated that
, say, had indicated that 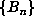 did not have a small period, our program continued to compute
did not have a small period, our program continued to compute 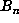 up to
up to 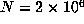 without employing Floyd's algorithm. If the last record occurred for
without employing Floyd's algorithm. If the last record occurred for 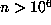 , then this was larger than could have been obtained from Floyd's algorithm and the
cost was less than
, then this was larger than could have been obtained from Floyd's algorithm and the
cost was less than 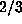 the cost of using that algorithm. On the other hand, in those
rare cases where the last record occurred for
the cost of using that algorithm. On the other hand, in those
rare cases where the last record occurred for 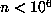 , the computation was repeated
using Floyd's algorithm and a relatively small
, the computation was repeated
using Floyd's algorithm and a relatively small 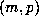 was usually detected.
For example, with
was usually detected.
For example, with 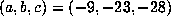 , a computation up to
, a computation up to 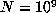 indicated
that the last record occurred at n = 1782995, suggesting a periodic sequence. A
recomputation of
indicated
that the last record occurred at n = 1782995, suggesting a periodic sequence. A
recomputation of 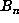 in the range
in the range 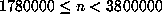 found the values
found the values 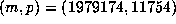 .
.
As mentioned above, a list was maintained of values of 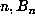 for which the
computation of
for which the
computation of 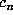 required quadruple precision. Let us call these n markers.
Suppose one has computed
required quadruple precision. Let us call these n markers.
Suppose one has computed 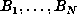 , where N > m+2p, and that one of these
markers,
, where N > m+2p, and that one of these
markers, 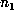 , occurs within the periodic part of the sequence, that is, for
, occurs within the periodic part of the sequence, that is, for 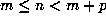 . Then, by periodicity,
. Then, by periodicity, 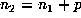 must be a marker and thus must occur within
the list of markers. Thus, by scanning this list of
must be a marker and thus must occur within
the list of markers. Thus, by scanning this list of 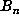 for
repeats, one can obtain p directly, as well as an upper bound on m. A recomputation
of
for
repeats, one can obtain p directly, as well as an upper bound on m. A recomputation
of 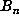 in a short range enables one to compute m exactly.
in a short range enables one to compute m exactly.
For example, with 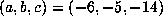 , we computed
, we computed 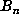 up to
up to 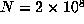 and determined that the last record occurred for n = 45622056, suggesting that the
sequence was possibly periodic. A check of the list of markers revealed that
and determined that the last record occurred for n = 45622056, suggesting that the
sequence was possibly periodic. A check of the list of markers revealed that 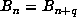 for n = 39667761 and n + q = 132886569, and that no marker k between
these values had
for n = 39667761 and n + q = 132886569, and that no marker k between
these values had 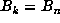 . Thus, the period was revealed to be p = q =
93218808. Since
. Thus, the period was revealed to be p = q =
93218808. Since 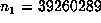 is a marker, but
is a marker, but 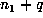 is not, the list also
showed that
is not, the list also
showed that 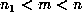 , and a binary search in this range revealed that m =
39420662.
, and a binary search in this range revealed that m =
39420662.
On the other hand, for 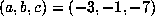 , we computed
, we computed 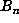 up to
up to 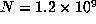 . The last record of
. The last record of 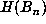 (which was 81363), occurred for n =
1199978517, giving the lower bound for D = m + p listed in
Table 2
. The
computation of
(which was 81363), occurred for n =
1199978517, giving the lower bound for D = m + p listed in
Table 2
. The
computation of 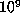 values of
values of  required
required 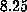 hours of CPU time on the Amdahl
5860. Even if
hours of CPU time on the Amdahl
5860. Even if  , it does not seem practical to compute p in this case by
a direct approach unless p should happen to be quite small relative to m+p.
, it does not seem practical to compute p in this case by
a direct approach unless p should happen to be quite small relative to m+p.
In addition to the markers, a table of 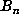 for multiples
of
for multiples
of 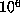 was also maintained, so that the computation could be restarted from any such
value without having to recompute the entire sequence. Although the markers here arose
in a natural way from the algorithm employed, one could clearly also use some more
artificial criterion for inventing markers. For example, one could store all those
pairs
was also maintained, so that the computation could be restarted from any such
value without having to recompute the entire sequence. Although the markers here arose
in a natural way from the algorithm employed, one could clearly also use some more
artificial criterion for inventing markers. For example, one could store all those
pairs 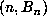 with the first component of
with the first component of 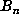 divisible by 1000. Then, in a
computation up to
divisible by 1000. Then, in a
computation up to 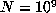 one would expect about
one would expect about 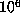 values of
values of 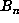 to be stored,
and that one of these values would occur within the period unless p was unusually
small.
to be stored,
and that one of these values would occur within the period unless p was unusually
small.