![[Shownotes]](../gif/annotate/shide-21.gif)
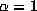 but it clearly applies to general rational
but it clearly applies to general rational  . Writing
. Writing 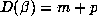 for
the size of the orbit
for
the size of the orbit 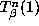 , the
argument correctly predicts that
, the
argument correctly predicts that 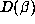 will be small relative to
will be small relative to 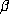 for Salem
numbers of degree 4. It predicts that
for Salem
numbers of degree 4. It predicts that 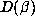 will be finite for almost all Salem
numbers of degree 6 but that
will be finite for almost all Salem
numbers of degree 6 but that 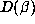 can be arbitrarily large
even for small
can be arbitrarily large
even for small 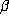 . Moreover, it predicts that for each fixed even degree
. Moreover, it predicts that for each fixed even degree 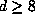 there should be a positive proportion of Salem numbers of degree d for which
there should be a positive proportion of Salem numbers of degree d for which 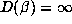 , as well as a positive proportion for which
, as well as a positive proportion for which 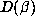 is finite. This latter prediction has
not yet been tested by extensive experiment.
is finite. This latter prediction has
not yet been tested by extensive experiment.
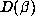 is directly related to the size of
is directly related to the size of  . Here
. Here
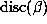 denotes the discriminant of the polynomial P. We explore this
connection through some of the computed examples for d = 6.
denotes the discriminant of the polynomial P. We explore this
connection through some of the computed examples for d = 6.
For Schmidt's more general conjecture the model predicts that if d = 4, the size of the
orbit 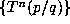 for fixed
for fixed 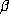 should be roughly proportional to
should be roughly proportional to 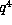 . This has
also not been extensively tested.
. This has
also not been extensively tested.
If 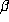 is a Salem number of degree d = 2s, then it has two real conjugates,
is a Salem number of degree d = 2s, then it has two real conjugates,
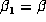 and
and 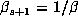 , and s-1 pairs of complex conjugates
, and s-1 pairs of complex conjugates
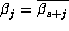 for
for 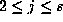 . All the numbers
. All the numbers 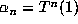 lie in the set
lie in the set 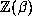 . As is familiar from the geometry of numbers we
can think of
. As is familiar from the geometry of numbers we
can think of 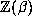 as a lattice L in
as a lattice L in 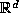 defined by mapping
defined by mapping
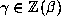 onto the point
onto the point 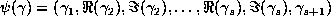 , where
, where 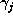 denotes the conjugate of
denotes the conjugate of 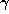 corresponding to the conjugation
corresponding to the conjugation 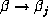 .
The determinant of L is
.
The determinant of L is
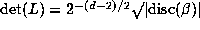 , since there are d-2 nonreal
conjugates, where
, since there are d-2 nonreal
conjugates, where 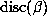 denotes the discriminant of the order
denotes the discriminant of the order 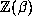 i.e., the discriminant of the minimal polynomial P of
i.e., the discriminant of the minimal polynomial P of 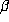 . Thus, the number of
points of L in a large cube of volume V is asymptotically
. Thus, the number of
points of L in a large cube of volume V is asymptotically 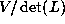 .
.
Now, consider the iterates 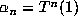 as points in the lattice
L. By definition,
as points in the lattice
L. By definition, 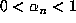 . The conjugate
. The conjugate 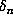 of
of 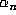 corresponding to
corresponding to 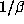 is
is 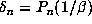 , which satisfies
, which satisfies
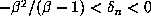 . For a typical conjugate
. For a typical conjugate 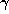 with
with 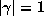 , the corresponding conjugate of
, the corresponding conjugate of 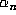 is
is 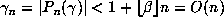 . However, it is reasonable to expect that
. However, it is reasonable to expect that 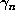 may
be
may
be 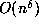 for some
for some  . In fact, a random walk argument makes it plausible
that
. In fact, a random walk argument makes it plausible
that 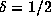 .
.
For example,
Figure 1
shows the first 50000 values of
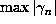 for the case
for the case 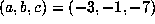 , which suggests some sort of random
process. A fit of a power curve to this data (the solid curve in
Figure 1
) suggests an
exponent
, which suggests some sort of random
process. A fit of a power curve to this data (the solid curve in
Figure 1
) suggests an
exponent 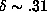 . However, using the data up to
. However, using the data up to 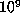 suggests an exponent in
the range
suggests an exponent in
the range 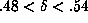 , consistent with
, consistent with 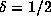 .
Figure 2
shows the case
.
Figure 2
shows the case 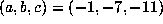 , where
, where 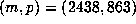 . For the initial transient,
. For the initial transient, 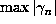 is well fitted for
is well fitted for 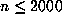 by a curve
by a curve 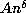 with
with 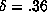 .
.
The points 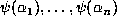 of L lie in a
slab
of L lie in a
slab 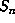 which is the product of two intervals of bounded length, corresponding to
the conjugates
which is the product of two intervals of bounded length, corresponding to
the conjugates 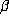 and
and 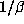 , and
, and 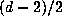 disks of radius
disks of radius 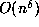 corresponding to the conjugates
corresponding to the conjugates 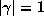 . The volume of
. The volume of 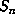 is
is
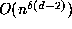 , which is
, which is 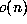 if
if 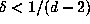 .
. 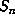 contains
contains 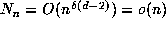 points of L by a result of Senechal and de Bruijn [8,]. (This result was not used in [4], where the conclusion that
points of L by a result of Senechal and de Bruijn [8,]. (This result was not used in [4], where the conclusion that 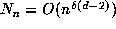 is presented as being merely plausible. It is in fact rigorously
justified). For each n, the n points
is presented as being merely plausible. It is in fact rigorously
justified). For each n, the n points 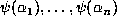 lie in
the set
lie in
the set 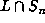 of size
of size 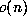 , so eventually there must be a coincidence between two
points with distinct indices, by the box principle, and hence the orbit must be periodic.
Note that, even for d = 4,
this argument would require
, so eventually there must be a coincidence between two
points with distinct indices, by the box principle, and hence the orbit must be periodic.
Note that, even for d = 4,
this argument would require 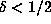 , and we expect that in fact
, and we expect that in fact 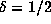 .
For d = 6, we would need
.
For d = 6, we would need 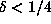 , which does not seem reasonable.
, which does not seem reasonable.
If we go beyond the box principle and imagine that
the points of the orbit 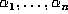 are distributed ``randomly'' in the
slab
are distributed ``randomly'' in the
slab 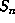 , we can allow a larger value of
, we can allow a larger value of 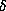 by making use of the ``birthday
paradox''. Suppose
that
by making use of the ``birthday
paradox''. Suppose
that 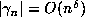 with
with 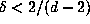 , so the volume
, so the volume 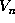 of
of 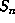 satisfies
satisfies 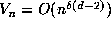 and hence
and hence 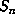 contains
contains 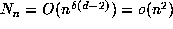 points of the lattice L. Now suppose that the points
points of the lattice L. Now suppose that the points
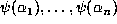 are randomly chosen from these
are randomly chosen from these 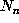 points.
Then the ``probability'' that these n are distinct is
points.
Then the ``probability'' that these n are distinct is

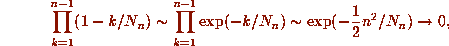 as
as  since
since 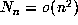 .
.
For d = 4, this argument requires  , which is just short of what can be
proved, while for d = 6, the requirement is
, which is just short of what can be
proved, while for d = 6, the requirement is 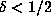 , which is just short of the
, which is just short of the
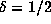 suggested by random walk. For
suggested by random walk. For 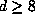 ,
however, even the most favorable assumptions would not seem to justify the expectation
that the orbit
,
however, even the most favorable assumptions would not seem to justify the expectation
that the orbit 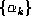 should be finite.
should be finite.
Let us now assume that indeed 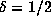 , and that
, and that 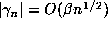 ,
where the O constant is uniform in
,
where the O constant is uniform in 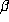 . The region
. The region 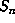 , being the product of two
intervals of lengths 1 and
, being the product of two
intervals of lengths 1 and 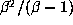 and
and 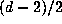 disks of radius
disks of radius 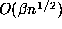 , has volume
, has volume 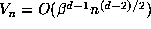 . Since the points of L
are distributed with density
. Since the points of L
are distributed with density 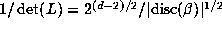 there are
there are 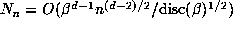 points of L in
points of L in
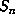 . If
. If 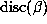 is sufficiently large, it is thus possible to push through the
box principle argument for d = 4 and the birthday paradox argument for d = 6
to conclude that the orbit of
is sufficiently large, it is thus possible to push through the
box principle argument for d = 4 and the birthday paradox argument for d = 6
to conclude that the orbit of 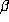 should be finite. For d = 8, these assumptions
lead to the conclusion that
should be finite. For d = 8, these assumptions
lead to the conclusion that 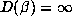 for a positive proportion of
for a positive proportion of 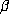 .
Being more precise, one finds that
.
Being more precise, one finds that
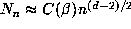 , where
, where

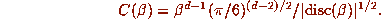 One can make plausible arguments that typically
One can make plausible arguments that typically 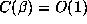 . Values of
. Values of
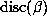 which are untypically small will lead to large values of
which are untypically small will lead to large values of 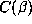 .
.
It turns out that the cases d = 4 and d = 6 in which we expect 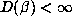 are distinguised by the expected size of the orbit
are distinguised by the expected size of the orbit 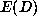 :
:
For d =4, the prediction is that

 which is somewhat smaller than rigorously proved in [2] for
which is somewhat smaller than rigorously proved in [2] for 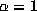 .
On the other hand, if d = 6, we find that
.
On the other hand, if d = 6, we find that

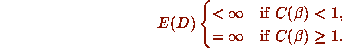
The data for 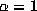 described in [4] tends to confirm a direct relationship
between the sizes of
described in [4] tends to confirm a direct relationship
between the sizes of 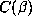 and
and 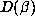 , although not quite as dramatic as this.
, although not quite as dramatic as this.
The extension of the argument from 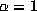 to
to 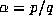 is straightforward. The
only change is that the orbit now lies in the lattice
is straightforward. The
only change is that the orbit now lies in the lattice
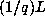 with density
with density 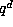 times as large as the density of L. Thus the
qualitative predictions of are unchanged, so we predict that Schmidt's
conjecture is true for Salem numbers of degree 4 and 6 but not for higher degrees.
Quantitatively, the replacement of
times as large as the density of L. Thus the
qualitative predictions of are unchanged, so we predict that Schmidt's
conjecture is true for Salem numbers of degree 4 and 6 but not for higher degrees.
Quantitatively, the replacement of 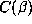 by
by 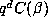 . suggests that, for d =
4 the size of the orbit should be roughly proportional to
. suggests that, for d =
4 the size of the orbit should be roughly proportional to 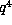 , and for d = 6 we should
expect unusually large orbits as soon as
, and for d = 6 we should
expect unusually large orbits as soon as 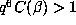 . It would be interesting to
test these predictions by further computation.
. It would be interesting to
test these predictions by further computation.