![[Shownotes]](../gif/annotate/sshow-11.gif)
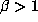 , the beta transformation
, the beta transformation 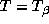 is
defined for
is
defined for 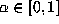 by
by 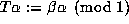 .
If
.
If 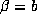 is an integer and if
is an integer and if

 is the b-ary expansion of
is the b-ary expansion of  , then the action of T on
, then the action of T on  is easily
described:
is easily
described:

 That is, T acts as a one-sided shift on the sequence of b-ary digits of
That is, T acts as a one-sided shift on the sequence of b-ary digits of  .
.
If 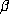 is not an integer, we can use T to set up an expansion for
which the above description is still valid. Define
is not an integer, we can use T to set up an expansion for
which the above description is still valid. Define 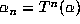 and
and
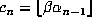 . Then
. Then 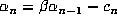 ,
for
,
for 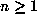 . Clearly,
. Clearly, 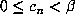 for all n, and
for all n, and

 We will refer to the sequence
We will refer to the sequence 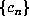 as the beta expansion of
as the beta expansion of  to base
to base
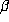 .
.
Here is some code to compute the beta expansion of alpha (and evaluate the above sum).
One distinction between integer and non-integer bases is that, in the latter case,
not every possible sequence 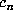 is a possible expansion.
Parry [5] gave a simple criterion for which sequences can occur:
Let
is a possible expansion.
Parry [5] gave a simple criterion for which sequences can occur:
Let 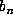 be the modified beta expansion of 1 defined as above, except that the
fractional part is taken to be in
be the modified beta expansion of 1 defined as above, except that the
fractional part is taken to be in 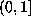 rather than
rather than 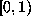 . This prevents the
expansion from ending in an infinite sequence of zeros. Then
. This prevents the
expansion from ending in an infinite sequence of zeros. Then 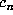 is the expansion
of some
is the expansion
of some  in
in 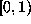 if and only if
if and only if 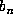 dominates
dominates 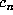 in the
sense of lexicographic order. Another point is that if
in the
sense of lexicographic order. Another point is that if 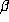 is not an integer
there can be infinitely many expressions of
is not an integer
there can be infinitely many expressions of  as a sum (1.3) with all
as a sum (1.3) with all 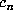 satisfying
satisfying 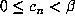 . The expansion we have singled out is the
``greedy'' expansion.
. The expansion we have singled out is the
``greedy'' expansion.
You can verify this lack of uniqueness for yourself in case
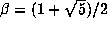 is the golden ratio. Notice that the relation
is the golden ratio. Notice that the relation
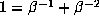 enables one to replace a word 100 in such an expansion
by 011. So clearly some numbers will have uncountably many expansions to this
base, but only one of these is the beta expansion.
enables one to replace a word 100 in such an expansion
by 011. So clearly some numbers will have uncountably many expansions to this
base, but only one of these is the beta expansion.
Recall the familiar argument which shows the periodicity of the b expansion of
a rational number 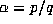 . It is clear that all the numbers
. It is clear that all the numbers 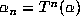 are of the form
are of the form 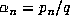 with
with 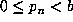 . Since there are only a finite
number of possibilities for
. Since there are only a finite
number of possibilities for 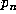 , there must be a repetition in the sequence
, there must be a repetition in the sequence
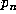 and hence in the sequence
and hence in the sequence 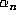 . But
. But 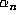 determines
determines 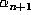 uniquely,
and hence
uniquely,
and hence 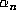 is periodic and thus
is periodic and thus 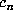 is periodic.
is periodic.
Let us consider whether there could be non-integers 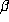 with the same property.
It is easy to see by induction that
with the same property.
It is easy to see by induction that 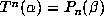 , where
, where

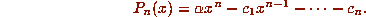 Thus, if the expansion of
Thus, if the expansion of  is periodic, so that
is periodic, so that 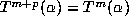 , with
the period length p and preperiod length m chosen minimally, then
, with
the period length p and preperiod length m chosen minimally, then 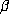 satisfies the
polynomial equation
satisfies the
polynomial equation 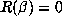 , where
, where

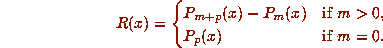 In particular, if the expansion of 1 is periodic then
In particular, if the expansion of 1 is periodic then 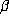 is an algebraic integer
whose minimal polynomial
is an algebraic integer
whose minimal polynomial 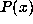 divides
divides 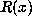 .
The following code computes beta from its expansion
.
The following code computes beta from its expansion
However, it does not seem likely at first glance that 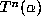 would be periodic
if
would be periodic
if 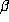 is a non-rational algebraic integer. It is clear that all of the numbers
is a non-rational algebraic integer. It is clear that all of the numbers
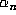 are in the ring
are in the ring 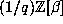 , i.e. of the form
, i.e. of the form

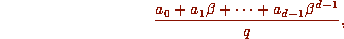 where d is the degree of
where d is the degree of 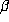 . But the set of expressions of this form
is dense in
. But the set of expressions of this form
is dense in 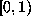 so the argument which worked for integer
so the argument which worked for integer 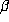 does
not seem to apply.
does
not seem to apply.
Recall that a
Pisot number
(or Pisot-Vijayaraghavan number, or PV
number) is an algebraic integer 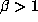 for which all conjugates
for which all conjugates 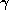 of
of
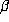 with
with 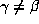 satisfy
satisfy 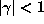 . (The conjugates are
the roots of the minimal polynomial). For
example, the golden ratio is a Pisot number since its conjugate
. (The conjugates are
the roots of the minimal polynomial). For
example, the golden ratio is a Pisot number since its conjugate 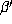 satisfies
satisfies
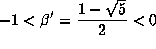 . There are Pisot numbers of every degree,
in fact there are such numbers in every number field.
. There are Pisot numbers of every degree,
in fact there are such numbers in every number field.
Bertrand [1] and Schmidt [7] independently showed that if  is rational
and
is rational
and 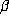 is a Pisot number then
is a Pisot number then 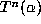 is periodic. It makes sense to test this
somewhat unexpected result with a few experiments. For example, take
is periodic. It makes sense to test this
somewhat unexpected result with a few experiments. For example, take 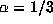 and
and 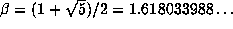 . This is easy to try numerically on a pocket
calculator, or using Maple, and we find the values for
. This is easy to try numerically on a pocket
calculator, or using Maple, and we find the values for 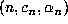 for
for 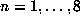 shown in
Table 1.
This certainly suggests that the expansion is purely periodic with period 8.
We can verify this by carrying out the calculation in the ring
shown in
Table 1.
This certainly suggests that the expansion is purely periodic with period 8.
We can verify this by carrying out the calculation in the ring 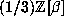 ,
or let Maple do it and obtain the exact values for
,
or let Maple do it and obtain the exact values for 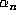 shown in
Table 2.
shown in
Table 2.
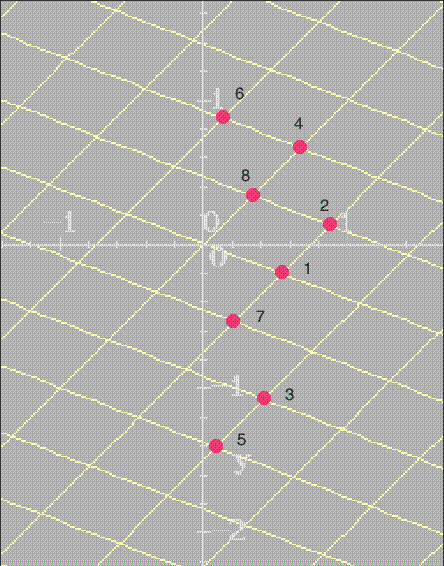
Why is this periodic? The result becomes less mysterious if we realize that the
numbers 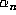 listed in
Table 2
are the projections onto the real axis of points
in the
lattice
listed in
Table 2
are the projections onto the real axis of points
in the
lattice
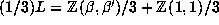 , i.e. the set of integer
combinations of
, i.e. the set of integer
combinations of 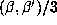 and
and 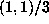 . Since
. Since 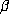 is irrational, the
set of such projections is dense in
is irrational, the
set of such projections is dense in 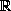 , so why does the above orbit only
meet finitely many of these lattice points? This is where the condition that
, so why does the above orbit only
meet finitely many of these lattice points? This is where the condition that
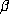 be a Pisot number is used. Notice that the conjugate of
be a Pisot number is used. Notice that the conjugate of  is
is 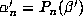 . But since
. But since 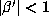 and all
and all 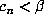 , we have
, we have

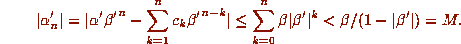 So, we are only dealing with a finite portion of the lattice
So, we are only dealing with a finite portion of the lattice  , namely that
contained in the rectangle
, namely that
contained in the rectangle  , and this is only a finite set
of lattice points.
, and this is only a finite set
of lattice points.
The following code enables you to change the values of beta and alpha.
It is clear how this argument extends to any rational  and any Pisot number
and any Pisot number 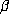 .
The only difference is that if
.
The only difference is that if 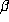 has degree d, we are dealing with a lattice in
has degree d, we are dealing with a lattice in
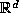 . The bounds one obtains on the size of the orbit are quite large and do not
suggest the many patterns one observes in practice. For a discussion of the
expansions for Pisot numbers in
. The bounds one obtains on the size of the orbit are quite large and do not
suggest the many patterns one observes in practice. For a discussion of the
expansions for Pisot numbers in  , and an answer to the question of whether
the
complementary factor
, and an answer to the question of whether
the
complementary factor
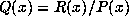 need be cyclotomic, see
[3].
need be cyclotomic, see
[3].
As mentioned above, Schmidt showed that if the 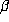 -expansion of every rational is
periodic then
-expansion of every rational is
periodic then 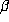 must be a Pisot or a
Salem number
. Recall here that a
Salem number
is an algebraic integer such that all conjugates
must be a Pisot or a
Salem number
. Recall here that a
Salem number
is an algebraic integer such that all conjugates 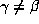 satisfy
satisfy
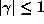 with at least one case of equality. This implies that
with at least one case of equality. This implies that 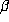 is
reciprocal, so
is
reciprocal, so 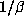 is a conjugate of
is a conjugate of 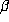 and the minimal polynomial of
and the minimal polynomial of 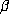 is a reciprocal (palendromic) polynomial of even degree.
Schmidt's conjecture is that the converse of this theorem is true, that is that
if
is a reciprocal (palendromic) polynomial of even degree.
Schmidt's conjecture is that the converse of this theorem is true, that is that
if 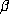 is a Salem number, then the
is a Salem number, then the 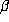 -expansion of every rational is periodic.
-expansion of every rational is periodic.
The smallest degree for Salem numbers is 4.
The behaviour of the preperiod and period lengths is quite tame in this case,
as one can see from
Table 3.
, which gives the period and preperiod for each
Salem number of degree 4 and trace 10. Each such number is identified by
the middle coefficient of the minimal polynomial, i.e. 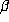 satisfies
satisfies
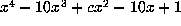 .
.
Click here
to compute the first few terms of the Beta Expansion of a degree 4
Salem number from its minimal polynomial 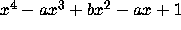 .
.
The pattern observed in
Table 3.
is general, as we showed in [2], where we
proved Schmidt's conjecture for 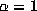 and all Salem numbers of degree 4
(so
and all Salem numbers of degree 4
(so 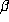 is a beta number in Parry's terminology).
The general conjecture remains open even for degree 4. The method used in
[2] could likely be extended to other rationals with small denominators
but it is unlikely to succeed for all rational
is a beta number in Parry's terminology).
The general conjecture remains open even for degree 4. The method used in
[2] could likely be extended to other rationals with small denominators
but it is unlikely to succeed for all rational  .
Explicitly, if
.
Explicitly, if 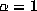 , then in all cases m = 1, i.e.,
, then in all cases m = 1, i.e., 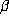 (mod 1) is a purely
periodic point of T. If
(mod 1) is a purely
periodic point of T. If 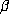 has the minimal polynomial
has the minimal polynomial 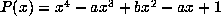 , then for fixed a the period
, then for fixed a the period 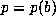 is a unimodal function of b and
takes on values which lie in the set
is a unimodal function of b and
takes on values which lie in the set 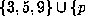 even
even 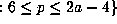 .
Thus,
.
Thus, 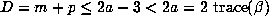 for all Salem numbers of degree 4.
No such bound seems to be true for Salem numbers of higher degree, even for
for all Salem numbers of degree 4.
No such bound seems to be true for Salem numbers of higher degree, even for 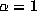 .
.
In contrast, for degree 6, we find a much more interesting behaviour, as one sees
by inspecting the
tables
in [4].
Table 4
reproduces some of that data
for the Salem numbers with minimal polynomials
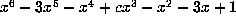 . In all cases but one, m = 1 and
. In all cases but one, m = 1 and 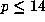 .
But for c = -7, we have only been able to show that m + p > 1199978517, so the orbit
in this case is very large, possibly infinite. Clearly c = -7 is notable not only for
the size of its orbit but also the size of
.
But for c = -7, we have only been able to show that m + p > 1199978517, so the orbit
in this case is very large, possibly infinite. Clearly c = -7 is notable not only for
the size of its orbit but also the size of 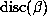 . Our discussion below will
indicate why a small value of
. Our discussion below will
indicate why a small value of 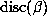 should be expected to lead to a large value
of m + p. More precisely, we suggest a relation between the size of the orbit and
the size of
should be expected to lead to a large value
of m + p. More precisely, we suggest a relation between the size of the orbit and
the size of 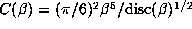 .
.
Click here
to compute the first few terms of the Beta Expansion of a degree 6
Salem number from its minimal polynomial 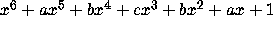 .
.
At first it is natural to suspect that in this case the orbit is infinite. In order to
understand why we now feel this is not the case, we must consider the probabilistic
model presented below and, in more detail, in [4]. What we believe is true
here is that m and p are simply very large. Such large periods are possible.
For example, for the Salem number with minimal polynomial
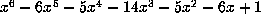 , the preperiod and period of the
orbit of 1 are m = 39420662 and p = 93218808. For other large values of m+p, see
Table 2
of [4].
, the preperiod and period of the
orbit of 1 are m = 39420662 and p = 93218808. For other large values of m+p, see
Table 2
of [4].
There are 11836 Salem numbers of degree 6 and trace at most 15. We have computed
the complete expansion for all but 80 of these. For the most part there is a great
deal of regularity in the distribution of 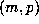 , and the values of m and p are quite
small: for all but 199 of the numbers surveyed, both m < 1000 and p < 1000. For
9609 of the numbers (81% of the total) we have m = 1, but, in contrast to the
degree-4 situation, larger values of m do occur with a certain regularity. However,
among the remaining 199 cases, there are at least 79 for which
, and the values of m and p are quite
small: for all but 199 of the numbers surveyed, both m < 1000 and p < 1000. For
9609 of the numbers (81% of the total) we have m = 1, but, in contrast to the
degree-4 situation, larger values of m do occur with a certain regularity. However,
among the remaining 199 cases, there are at least 79 for which 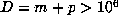 and
at least two for which
and
at least two for which 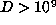 .
.
Our probabilistic model suggests that m + p will be large if 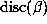 is small
relative to
is small
relative to 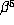 .
A competing explanation might be that some peculiar arithmetic relation between the
conjugates of
.
A competing explanation might be that some peculiar arithmetic relation between the
conjugates of 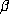 on the unit circle is the cause of the large orbits. To see that
this is not the case, consider the orbits of 1 when
on the unit circle is the cause of the large orbits. To see that
this is not the case, consider the orbits of 1 when 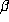 is a power of the smallest
Salem number
is a power of the smallest
Salem number 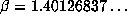 of degree 6, which has minimal polynomial
of degree 6, which has minimal polynomial 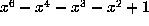 . This data is given in
Table 5.
. The correlation between the large
values of m+p and the large values of
. This data is given in
Table 5.
. The correlation between the large
values of m+p and the large values of 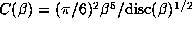 is evident.
is evident.