![[Shownotes]](../gif/annotate/shide-101.gif)
The Gauss map preserves the Gauss measure

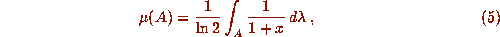 where
where 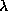 is the Lebesgue measure. Thus the Gauss map is
ergodic, and almost all (in the sense of either the Lebesgue
or Gauss measure) initial points have orbits which have the
interval
is the Lebesgue measure. Thus the Gauss map is
ergodic, and almost all (in the sense of either the Lebesgue
or Gauss measure) initial points have orbits which have the
interval 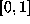 as
as  -limit set. Thus the only
attractor whose basin of attraction
has nonzero measure is the
interval
-limit set. Thus the only
attractor whose basin of attraction
has nonzero measure is the
interval 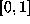 . By the ergodicity of the map, we may explicitly
calculate the Lyapunov exponent as follows:
. By the ergodicity of the map, we may explicitly
calculate the Lyapunov exponent as follows:

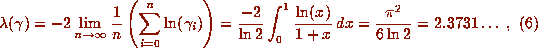 which holds for almost all initial points
which holds for almost all initial points 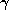 . This is of interest,
since there are few nontrivial maps for which the Lyapunov exponent
can be calculated explicitly.
. This is of interest,
since there are few nontrivial maps for which the Lyapunov exponent
can be calculated explicitly.
This section, more than any other in the paper, provoked puzzlement
on the part of readers of the original. The original purpose was to
show the reader how powerful ergodic methods were: in one line
we establish the `almost-everywhere' value of the Lyapunov exponent
for the Gauss map, using the ergodic result that the `time-average'
of 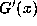 along the
orbit is equal to the (properly-weighted) `space-average' given
by the integral of
along the
orbit is equal to the (properly-weighted) `space-average' given
by the integral of 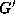 with respect to the Gauss measure.
with respect to the Gauss measure.
I have since also learned that this Lyapunov exponent can
be explicitly connected with Khintchin's constant (mentioned
previously as the geometric mean of the partial
quotients, which
turns out to be the same for almost all x in 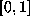 ).
Khintchin's constant is K, where
).
Khintchin's constant is K, where 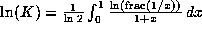 .
(By the same arguments). The only difference is the
presence of the `fractional part'.
This integral gives a simple convergent series
for
.
(By the same arguments). The only difference is the
presence of the `fractional part'.
This integral gives a simple convergent series
for 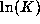 which can be transformed into a quickly convergent one.
(The integral becomes a series because frac(1/x) is piecewise
constant). See [7] for details.
which can be transformed into a quickly convergent one.
(The integral becomes a series because frac(1/x) is piecewise
constant). See [7] for details.