![[Shownotes]](../gif/annotate/sshow-111.gif)
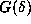 is computed as 0, whenever
is computed as 0, whenever
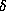 is any number between 0 and u. This effectively
limits the power of the singularity of the Gauss map.
Click here for further remarks on the machine epsilon u.
is any number between 0 and u. This effectively
limits the power of the singularity of the Gauss map.
Click here for further remarks on the machine epsilon u.
To return to the analogy of the introduction, we consider the domain
of machine representable numbers not as a smooth circle but as a
slotted ring, with the number of slots on the ring corresponding to
the number of machine-representable numbers in the interval 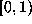 ,
where all numbers in
,
where all numbers in 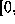 u
u are ``lumped together''.
In this analogy, u corresponds to the approximate width of
the slots. Now our bead can occupy one of the slots on the ring,
and not just any arbitrary position, and the floating-point Gauss
map takes the bead from one slot, winding around the ring as
many times as are indicated by the integer part, and finally putting
the bead into another slot. We see now that the maximum winding
number of the floating-point Gauss map is finite, and the slot next
to the origin is the one with this winding number.
are ``lumped together''.
In this analogy, u corresponds to the approximate width of
the slots. Now our bead can occupy one of the slots on the ring,
and not just any arbitrary position, and the floating-point Gauss
map takes the bead from one slot, winding around the ring as
many times as are indicated by the integer part, and finally putting
the bead into another slot. We see now that the maximum winding
number of the floating-point Gauss map is finite, and the slot next
to the origin is the one with this winding number.
A more evident difficulty is that all the representable points are rational, and we know that the exact Gauss map takes these initial points to zero eventually. So if we define a floating-point Gauss map as

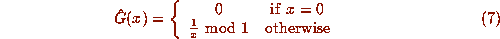 where now the operations of division and ``mod 1'' take place over
the floating-point domain, with attendant roundoff error, we have to
answer some new dynamical questions.
where now the operations of division and ``mod 1'' take place over
the floating-point domain, with attendant roundoff error, we have to
answer some new dynamical questions.
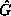 chaotic?
chaotic?
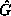 useful at all for study of G?
useful at all for study of G?
Not surprisingly, some orbits under 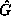 do terminate at 0, though
often not when we expect them to. However, on some machines, some orbits
never hit 0, being periodic. For example on the HP28S the initial
point
do terminate at 0, though
often not when we expect them to. However, on some machines, some orbits
never hit 0, being periodic. For example on the HP28S the initial
point 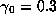 gives
gives 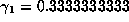 ,
,
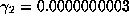 , and
, and 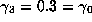 , with period
3. Note that under the exact Gauss map the second iterate (
, with period
3. Note that under the exact Gauss map the second iterate (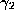 )
of this initial point is zero. Since the set of machine-representable
numbers is finite, all orbits are ultimately periodic (perhaps
with period 1, as at x=0). Note that the behaviour of
)
of this initial point is zero. Since the set of machine-representable
numbers is finite, all orbits are ultimately periodic (perhaps
with period 1, as at x=0). Note that the behaviour of 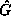 depends strongly on the floating-point implementation. For example,
with the Apple SANE numerics implementation, the starting point
depends strongly on the floating-point implementation. For example,
with the Apple SANE numerics implementation, the starting point 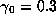 gives an orbit with either a long transient regime or a long period,
with no regularity detected in the first 65,000 elements of the orbit.
A Maple implementation of Floyd's algorithm for
finding when the cycle starts.
gives an orbit with either a long transient regime or a long period,
with no regularity detected in the first 65,000 elements of the orbit.
A Maple implementation of Floyd's algorithm for
finding when the cycle starts.
Since all orbits are ultimately periodic, and there are only a finite
number of such orbits, the floating-point Gauss map (and indeed any
machine simulation of any dynamical system) is not chaotic
in the usual sense. Arbitrarily small perturbations in the initial
conditions are not even allowed, so the sensitivity of the map to such
perturbations is moot. The alternate definition of S. I. C. requires arbitrarily
close initial conditions, which cannot happen in a finite set.
Similarly, the usual definition of the Lyapunov exponent for
the exact Gauss map seems not to be relevant here: the presence of the
derivative 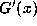 in the definition of the Lyapunov exponent measures the
effect of arbitrarily small perturbations. However, if we define
an approximate Lyapunov exponent for the first N iterations of the
floating point Gauss map as
in the definition of the Lyapunov exponent measures the
effect of arbitrarily small perturbations. However, if we define
an approximate Lyapunov exponent for the first N iterations of the
floating point Gauss map as

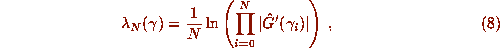 whenever the elements of the orbit are nonzero, then this in some sense
measures the average sensitivity of the first N elements of the
corresponding orbit under the exact Gauss map to arbitrarily
small perturbations. This ``Lyapunov exponent'' is what is calculated
in practice for a great many numerical simulations of dynamical systems,
and if it is positive this is taken as evidence for chaos in the
underlying system [10].
whenever the elements of the orbit are nonzero, then this in some sense
measures the average sensitivity of the first N elements of the
corresponding orbit under the exact Gauss map to arbitrarily
small perturbations. This ``Lyapunov exponent'' is what is calculated
in practice for a great many numerical simulations of dynamical systems,
and if it is positive this is taken as evidence for chaos in the
underlying system [10].
But what if the calculated orbit has no counterpart in the exact system? If roundoff errors introduced into the calculation produce an orbit that is unlike any in the exact system, this approximate Lyapunov exponent would be spurious. We will give a proof in the following section, which uses the techniques of floating-point error analysis, that shows orbits under the floating-point Gauss map are ``machine close'' to corresponding orbits under the exact Gauss map. A general theorem of this nature has been proved for hyperbolic invariant sets, by Bowen (see [10]). Here a direct proof is more appropriate and informative. This means that the approximate Lyapunov exponent defined above will accurately reflect the Lyapunov exponent of some orbit of the exact Gauss map, provided N is large enough that transient effects have been minimized, and not so large that accumulated roundoff error in the sum degrades the result. This is usually not a large problem.
We contrast this behaviour with what happens when continuous maps are
made discrete by (e.g.) finite difference schemes.
Yamaguti & Ushiki [29]
and Ushiki [28] have shown that finite difference formulae
applied to non-chaotic continuous systems may produce chaotic
numerical solutions if the stepsize is not too small, assuming
that the calculations are carried out exactly. In contrast
we have noted here that a chaotic discrete map becomes nonchaotic
when implemented in fixed-precision arithmetic.
A further difficulty is that all of the orbits of  are ultimately
periodic, and periodic orbits of G have Lyapunov exponents that are
different from the almost-everywhere value (which is usually the exponent
of physical interest).
are ultimately
periodic, and periodic orbits of G have Lyapunov exponents that are
different from the almost-everywhere value (which is usually the exponent
of physical interest).
It is not immediately clear that these Lyapunov exponents calculated
from  will tell us anything useful about the exact map G.
will tell us anything useful about the exact map G.
On closer examination, however, we see that if the period of an orbit is long, then the orbit behaves for a long time as if it were aperiodic, reflecting the effect of `nearby' initial points that are aperiodic.
Hence we may expect that the computed Lyapunov exponent of a long
period orbit will be close to 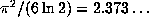 .
This is what happens in practice, since many initial points seem to give
long period orbits.
For example, if we compute the first 100,000 elements of the orbit
of
.
This is what happens in practice, since many initial points seem to give
long period orbits.
For example, if we compute the first 100,000 elements of the orbit
of 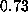 under
under 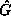 on the HP28S, we get a computed
on the HP28S, we get a computed
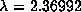 . This is within
. This is within 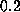 % of the expected value of
the Lyapunov exponent of the exact Gauss map.
Notice, though, that the Lyapunov exponent of the orbit of the exact
map G starting at
% of the expected value of
the Lyapunov exponent of the exact Gauss map.
Notice, though, that the Lyapunov exponent of the orbit of the exact
map G starting at 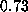 is not even defined---we rely
on the roundoff error to give us our results, which is somewhat unusual.
We will expand more on this in a later section.
is not even defined---we rely
on the roundoff error to give us our results, which is somewhat unusual.
We will expand more on this in a later section.