![[Shownotes]](../gif/annotate/sshow-31.gif)
The theory of continued fractions goes back at least to c. A. D.
500 to the work of  ryabhata, and possibly as far back as
c. 300 B.C. to Euclid. The theory of chaotic dynamical systems is
relatively recent, going back only to the work of
Poincaré [22] and
Birkhoff [2]. The foundations of the theory of continued fractions,
as we know it now, are well established due to the work of Euler, Lagrange,
Gauss, and others, while the foundations of chaotic dynamical systems are
still evolving. This paper will use the well-established theory of simple
continued fractions to explore some current results of the theory of chaotic
dynamical systems.
ryabhata, and possibly as far back as
c. 300 B.C. to Euclid. The theory of chaotic dynamical systems is
relatively recent, going back only to the work of
Poincaré [22] and
Birkhoff [2]. The foundations of the theory of continued fractions,
as we know it now, are well established due to the work of Euler, Lagrange,
Gauss, and others, while the foundations of chaotic dynamical systems are
still evolving. This paper will use the well-established theory of simple
continued fractions to explore some current results of the theory of chaotic
dynamical systems.
Olds [20] gives a good introduction to the classical theory of simple continued fractions, by which we mean continued fractions of the form

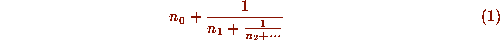 where the
where the 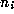 are all positive integers, except
are all positive integers, except 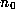 which may be zero
or negative. We will denote this as
which may be zero
or negative. We will denote this as 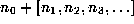 , and
in what follows
, and
in what follows 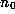 will usually be zero.
will usually be zero.
Simple continued fractions have found applications in Fabry-Perot
interferometry [13], and in the concept of noble
numbers
used in orbital stability and quasi-amorphous states of
matter [25].
For other uses of simple continued fractions in
chaos, see [8].
Other types of continued fraction exist, for
example, Gautschi [9], Henrici [12],
Jones and Thron [14], and others,
use functional or analytic continued fractions in approximation theory,
since analytic continued fractions can be very effective for computation.
We will not be concerned with such continued fractions. We will summarize
in the next section all the classical results that we need, without proof.
Proofs can be found in [20,11,19,15,1],
and [18].