![[Shownotes]](../gif/annotate/sshow-41.gif)
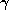 . We put
. We put 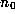 equal to the integer
part of
equal to the integer
part of 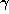 , by which we mean the greatest integer less than or
equal to
, by which we mean the greatest integer less than or
equal to 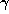 . If the fractional part of
. If the fractional part of 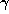 is not zero, we
put
is not zero, we
put 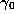 equal to the fractional part of
equal to the fractional part of 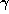 . We then
invert
. We then
invert 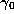 , and put
, and put 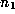 equal to the integer part of
equal to the integer part of 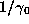 .
Similarly we put
.
Similarly we put 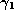 equal to the fractional part, and repeat.
Note that
equal to the fractional part, and repeat.
Note that 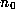 may be positive, negative, or zero, but that all the
subsequent
may be positive, negative, or zero, but that all the
subsequent 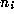 will be positive, and that each
will be positive, and that each 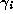 is in the
interval
is in the
interval 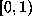 .
This process gives us a unique continued fraction for each starting point
.
This process gives us a unique continued fraction for each starting point
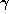 , and the process terminates if and only if
, and the process terminates if and only if 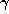 is rational.
(For any rational
is rational.
(For any rational  there is one other simple continued fraction, e.g.
there is one other simple continued fraction, e.g. 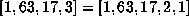 ,
which is only trivially different from the one generated by this algorithm.)
This algorithm is related to the Euclidean algorithm
for finding the
greatest common divisor (gcd)
of two integers k and m [20],
in that if we use this method to find the continued fraction of
,
which is only trivially different from the one generated by this algorithm.)
This algorithm is related to the Euclidean algorithm
for finding the
greatest common divisor (gcd)
of two integers k and m [20],
in that if we use this method to find the continued fraction of 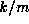 , then
the integer parts that arise are precisely the quotients from the
Euclidean algorithm, and in fact the last nonzero remainder from the
Euclidean algorithm appears as the numerator of the last nonzero
fractional part. This remainder is of course the gcd of k and m.
Further, this algorithm can easily be seen to terminate in
, then
the integer parts that arise are precisely the quotients from the
Euclidean algorithm, and in fact the last nonzero remainder from the
Euclidean algorithm appears as the numerator of the last nonzero
fractional part. This remainder is of course the gcd of k and m.
Further, this algorithm can easily be seen to terminate in 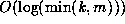 operations.
Click here for a
note on the above paragraph, 1995.
operations.
Click here for a
note on the above paragraph, 1995.
Classically, most attention has been paid to
the integers generated by this algorithm, which make up the continued
fraction itself. However, Gauss was apparently the first to study the
other part of this algorithm, which we present as the following map
from 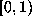 to
to 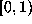 , called
the Gauss map [18] (see
FIGURE 1):
, called
the Gauss map [18] (see
FIGURE 1):

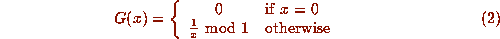
We use the notation ``mod 1'' to mean taking the fractional part. In terms of the Gauss map G, our algorithm then becomes

 (
(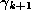 is undefined if
is undefined if 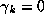 )
and we see that the continued fraction is generated as a byproduct of the
iteration of the Gauss map. Thus we expect that any classical results
on continued fractions will have implications for the dynamics of the Gauss
map.
)
and we see that the continued fraction is generated as a byproduct of the
iteration of the Gauss map. Thus we expect that any classical results
on continued fractions will have implications for the dynamics of the Gauss
map.
Note that the jump discontinuities occurring at 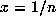 (for each positive integer
n) may all be removed by mapping onto the circle with the transformation
(for each positive integer
n) may all be removed by mapping onto the circle with the transformation
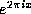 . After this is done, we see that the Gauss map (
. After this is done, we see that the Gauss map (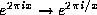 ) is a map of the circle onto the circle, and may be
pictured on a torus, as in
FIGURE 2.
Click here to examine a
Maple program for graphing arbitrary
) is a map of the circle onto the circle, and may be
pictured on a torus, as in
FIGURE 2.
Click here to examine a
Maple program for graphing arbitrary 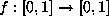 on the torus.
on the torus.
We make the following observation: if we represent a point in the
interval 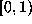 by its continued fraction,
by its continued fraction, 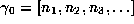 ,
then a simple induction shows that
,
then a simple induction shows that 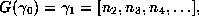
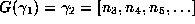 ,
, 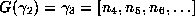 , and so on. This makes a connection
between the Gauss map and the
shift map of symbolic dynamics [8].
We will not explore this connection further here, but we note that
the shift maps normally studied are slightly different than the Gauss map,
in that here the size of the numbers in the list being ``shifted'' is
not bounded.
Click here for more
details on the induction.
, and so on. This makes a connection
between the Gauss map and the
shift map of symbolic dynamics [8].
We will not explore this connection further here, but we note that
the shift maps normally studied are slightly different than the Gauss map,
in that here the size of the numbers in the list being ``shifted'' is
not bounded.
Click here for more
details on the induction.
An analogy is illuminating: if we think of our space as a circular hoop
with the origin at one point O on the hoop, our initial point as a
dimensionless bead on the hoop, and the Gauss map as taking the bead from
its current position clockwise past O at least once to its next position
on the hoop, then the integers 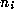 are the number of times the bead passes
O on the ith iteration (in general the maximum such number is called
the ``winding number'' of the map, and here this is obviously infinite),
and the
are the number of times the bead passes
O on the ith iteration (in general the maximum such number is called
the ``winding number'' of the map, and here this is obviously infinite),
and the 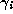 are the coordinates of the bead on the hoop once
it comes to rest. If the bead comes to rest close to the origin on one
side, with a small
are the coordinates of the bead on the hoop once
it comes to rest. If the bead comes to rest close to the origin on one
side, with a small 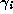 , then on the next iteration it will be pushed
many times around the hoop. If it comes to rest close to the origin on the
other side, with a
, then on the next iteration it will be pushed
many times around the hoop. If it comes to rest close to the origin on the
other side, with a 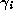 close to 1, then it will only go past the
origin once on its next iteration. We may think of the bead as being
pushed around the circle, with the strength of the push being inversely
proportional to the distance measured counterclockwise from the point O.
close to 1, then it will only go past the
origin once on its next iteration. We may think of the bead as being
pushed around the circle, with the strength of the push being inversely
proportional to the distance measured counterclockwise from the point O.