![[Shownotes]](../gif/annotate/sshow-21.gif)
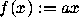 ,
where a>0. Given any initial point
,
where a>0. Given any initial point 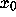 ,
it is clear that the dynamical system
,
it is clear that the dynamical system
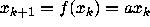 will have orbit
will have orbit

 Introduce a slight perturbation
Introduce a slight perturbation  to the initial
condition, say,
to the initial
condition, say, 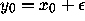 . The resulting orbit is:
. The resulting orbit is:

 So, after k iterations, these two orbits that started at
neighbouring points
So, after k iterations, these two orbits that started at
neighbouring points 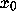 and
and 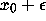 have separated
by
have separated
by 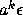 . Clearly, if 0<a<1, all orbits converge to zero.
For a=1, all points are fixed points of the map (f is the
identity map). For a>1, orbits diverge to infinity and,
choosing k sufficiently large, neighbouring initial points
have orbits that become arbitrarily far apart.
. Clearly, if 0<a<1, all orbits converge to zero.
For a=1, all points are fixed points of the map (f is the
identity map). For a>1, orbits diverge to infinity and,
choosing k sufficiently large, neighbouring initial points
have orbits that become arbitrarily far apart.
Since 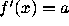 for any x, it follows that the
Lyapunov exponent of the linear map is the same
for any orbit, namely
for any x, it follows that the
Lyapunov exponent of the linear map is the same
for any orbit, namely 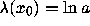 . The
Lyapunov exponent is negative if 0<a<1, in which
case all orbits converge to zero. When a>1,
the Lyapunov exponent is positive and the distance
between neighbouring orbits becomes arbitrarily large.
Hence,
. The
Lyapunov exponent is negative if 0<a<1, in which
case all orbits converge to zero. When a>1,
the Lyapunov exponent is positive and the distance
between neighbouring orbits becomes arbitrarily large.
Hence, 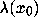 is related to the sensitivity
of orbits to perturbations. For
is related to the sensitivity
of orbits to perturbations. For 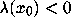 ,
neighbouring orbits remain close. However, when
a>1, even though
,
neighbouring orbits remain close. However, when
a>1, even though 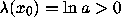 , the
system is not chaotic. This is due to the fact that the
system is unbounded for a>1. (Boundedness is
another requirement for chaos; this is better
illustrated by another example.)
, the
system is not chaotic. This is due to the fact that the
system is unbounded for a>1. (Boundedness is
another requirement for chaos; this is better
illustrated by another example.)