Contents Next: Example I: The Up: No Title Previous: No Title

Lyapunov Exponents

For a one dimensional discrete dynamical system

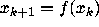with initial condition

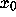, the Lyapunov exponent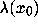

is defined as

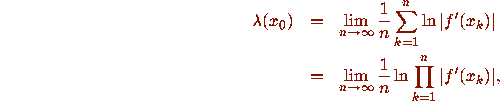whenever this limit exists. (Note that the Lyapunov exponent depends on the initial condition and hence varies for different orbits.)

Take the definition apart and look at the pieces for easier interpretation. For each k, 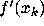tells how much the function f is changing with respect to its argument at the point 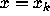. Since 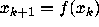, this derivative expresses the magnitude of change in the transition from 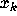to 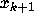. Taking the logarithm changes the scale on which the orbit is being studied. Finally, the limit of the average of the log of the derivatives over n iterations is taken to provide a measure of how fast the orbit changes as (discrete) time propagates. To summarise, the Lyapunov exponent contains information about the average rate of separation of neighbouring initial points. A positive Lyapunov exponent is an indication of chaotic behaviour.

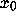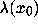Of course, the limit in question may not be easy to calculate. In practise, it is often helpful to use a ``finite time'' approximation to get some idea of what the Lyapunov exponent may be for a given orbit. Explicitly, for an orbit orb(), the finite time analog of the Lyapunov exponent is

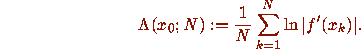The following examples and calculations are intended to illustrate these concepts more fully.

Contents Next: Example I: The Up: No Title Previous: No Title