![[Shownotes]](../gif/annotate/shide-11.gif)
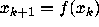 with initial condition
with initial condition 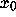 , the Lyapunov
exponent
, the Lyapunov
exponent 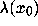 is defined as
is defined as

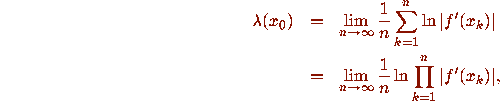 whenever this limit exists.
(Note that the Lyapunov exponent depends on the initial
condition and hence varies for different orbits.)
whenever this limit exists.
(Note that the Lyapunov exponent depends on the initial
condition and hence varies for different orbits.)
Take the definition apart and look at the pieces for
easier interpretation. For each k, 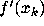 tells
how much the function f is changing with respect to
its argument at the point
tells
how much the function f is changing with respect to
its argument at the point 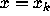 . Since
. Since 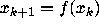 ,
this derivative expresses the magnitude of change
in the transition from
,
this derivative expresses the magnitude of change
in the transition from 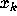 to
to 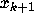 . Taking the logarithm
changes the scale on which the orbit is being studied. Finally,
the limit of the average of the log of the derivatives over
n iterations is taken to provide a measure of how fast
the orbit changes as (discrete) time propagates.
To summarise, the Lyapunov exponent contains information
about the average rate of separation of neighbouring initial
points. A positive Lyapunov exponent is an indication of
chaotic behaviour.
. Taking the logarithm
changes the scale on which the orbit is being studied. Finally,
the limit of the average of the log of the derivatives over
n iterations is taken to provide a measure of how fast
the orbit changes as (discrete) time propagates.
To summarise, the Lyapunov exponent contains information
about the average rate of separation of neighbouring initial
points. A positive Lyapunov exponent is an indication of
chaotic behaviour.
Of course, the limit in question may not be easy to calculate.
In practise, it is often helpful to use a ``finite time''
approximation to get some idea of what the Lyapunov exponent
may be for a given orbit.
Explicitly, for an orbit orb(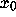 ), the finite
time analog of the Lyapunov exponent
), the finite
time analog of the Lyapunov exponent 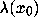 is
is

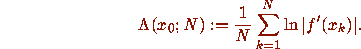 The following examples and calculations
are intended to illustrate these concepts more fully.
The following examples and calculations
are intended to illustrate these concepts more fully.