![[Shownotes]](../gif/annotate/shide-41.gif)

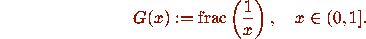 Since the map
Since the map 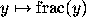 has as its derivative a ``sawtooth function'' with
slope 1, the discontinuous derivative of the Gauss map is
has as its derivative a ``sawtooth function'' with
slope 1, the discontinuous derivative of the Gauss map is

 provided
provided 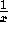 is not an integer. (The points
is not an integer. (The points
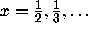 are points of
discontinuity of the Gauss map,
so its derivative obviously does not exist
at those points.)
are points of
discontinuity of the Gauss map,
so its derivative obviously does not exist
at those points.)
The following explorations are meant to convince you that the claims made about the Gauss map in this paper are in fact true. The links below will call up the Maple Form Interface. Please read the details in this document before calling up the Maple Form Interface if you are not familiar with Maple.
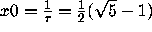 and N=5. Try changing x0 to
rational or irrational values. Verify that
and N=5. Try changing x0 to
rational or irrational values. Verify that
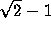 is a fixed point of the Gauss map.
(Various values are included in the code to simplify typing.
To use these values of x0, delete the # mark at the
beginning of the line with the desired value of x0 and
insert a # mark at the beginning of the previous value
assigned to x0. The # mark has the effect of
``commenting out'' a line of Maple code so that anything
to the right of # will be ignored when the code is executed.)
is a fixed point of the Gauss map.
(Various values are included in the code to simplify typing.
To use these values of x0, delete the # mark at the
beginning of the line with the desired value of x0 and
insert a # mark at the beginning of the previous value
assigned to x0. The # mark has the effect of
``commenting out'' a line of Maple code so that anything
to the right of # will be ignored when the code is executed.)
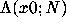 of the Lyapunov exponent of
an orbit orb(x0) of the Gauss map. Initially,
of the Lyapunov exponent of
an orbit orb(x0) of the Gauss map. Initially,
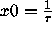 and N=200. Change x0 to various
rational, irrational and reduced quadratic irrational
values. Do the values of
and N=200. Change x0 to various
rational, irrational and reduced quadratic irrational
values. Do the values of 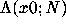 behave as expected?
(Various values are included in the code to simplify typing.
To use these values of x0, delete the # mark at the
beginning of the line with the desired value of x0 and
insert a # mark at the beginning of the previous value
assigned to x0. The # mark has the effect of
``commenting out'' a line of Maple code so that anything
to the right of # will be ignored when the code is executed.)
behave as expected?
(Various values are included in the code to simplify typing.
To use these values of x0, delete the # mark at the
beginning of the line with the desired value of x0 and
insert a # mark at the beginning of the previous value
assigned to x0. The # mark has the effect of
``commenting out'' a line of Maple code so that anything
to the right of # will be ignored when the code is executed.)