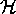 denote the complex upper half plane.
denote the complex upper half plane. 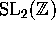 acts transitively
on
acts transitively
on 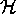 by linear fractional transformations
by linear fractional transformations
Let 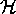 denote the complex upper half plane.
denote the complex upper half plane. 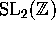 acts transitively
on
acts transitively
on 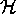 by linear fractional transformations
by linear fractional transformations

 Now we consider functions
Now we consider functions 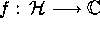 .
The notation
.
The notation
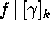 is used to denote the function whose value at
is used to denote the function whose value at  is
is
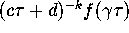 . The value of
. The value of
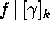 at
at  is denoted by
is denoted by 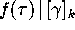 so that
so that

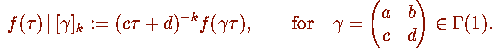 We define modular forms and cusp forms for a congruence subgroup
We define modular forms and cusp forms for a congruence subgroup
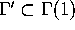 of level N. Let
of level N. Let 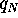 denote
denote 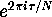 . Let
. Let 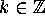 .
A function
.
A function 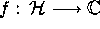 is said to
be a modular form of
weight k for
is said to
be a modular form of
weight k for 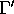 if
it satisfies the following conditions:
if
it satisfies the following conditions:
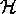 ,
,
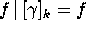 for all
for all 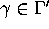 ,
,
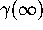 for
for
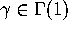 ; i.e.
; i.e. 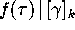 has the form
has the form
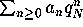 .
.
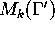 denote the set of such modular forms. It turns
out that
denote the set of such modular forms. It turns
out that 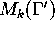 is a finite dimensional
is a finite dimensional  -vector
space.
If
-vector
space.
If 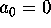 for all
for all 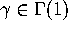 we say f is a cusp form.
We let
we say f is a cusp form.
We let 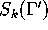 denote the subspace of cusp forms.
denote the subspace of cusp forms.
Now we define what it means for a function to be a modular form
of weight k and character 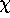 for the group
for the group 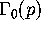 when p is prime.
Let
when p is prime.
Let 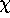 be a Dirichlet
character modulo p
be a Dirichlet
character modulo p

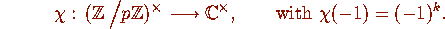 A function
A function 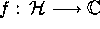 is said to
be a modular form of
weight k and character
is said to
be a modular form of
weight k and character 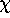 for
for 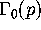 if it
satisfies conditions (i)--(iii) above except (ii) is replaced by
if it
satisfies conditions (i)--(iii) above except (ii) is replaced by

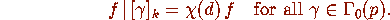 In this case, condition (iii) amounts to the following
two conditions:
In this case, condition (iii) amounts to the following
two conditions:

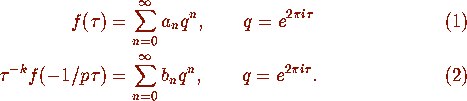 We call the Fourier series in (1) the q-expansion of f at
We call the Fourier series in (1) the q-expansion of f at 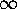 ,
and we call (2) the q-expansion at 0. We let
,
and we call (2) the q-expansion at 0. We let 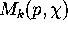 denote the
space of such modular forms.
If
denote the
space of such modular forms.
If 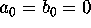 above then f is
a cusp form. We let
above then f is
a cusp form. We let 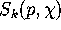 denote the subspace of
cusp forms.
denote the subspace of
cusp forms.