![[Shownotes]](../gif/annotate/shide-11.gif)
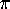 is a
quartic iteration due to J.M. and P.B. Borwein. In their paper,
the Borwein's show how this iteration and others are intimately connected
to the work of Ramanujan. This connection is shown utilizing
their alpha-function which is defined in terms of theta-functions.
They are able to find p-th order iterations based on this function
using modular equations for the theta-functions. In this paper
we construct an infinite family of functions
is a
quartic iteration due to J.M. and P.B. Borwein. In their paper,
the Borwein's show how this iteration and others are intimately connected
to the work of Ramanujan. This connection is shown utilizing
their alpha-function which is defined in terms of theta-functions.
They are able to find p-th order iterations based on this function
using modular equations for the theta-functions. In this paper
we construct an infinite family of functions 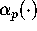 .
Each
.
Each 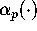 gives rise to a p-th order iteration. For p=4 we obtain a quartic iteration
due to the Borweins that does not come from the alpha-function.
For p=3 we obtain a cubic iteration
due to the Borweins that does not come from the alpha-function.
For p=7 we find a septic iteration that is analogous to
the cubic iteration. For p=9 we obtain a nonic (ninth order) iteration
that does not seem to come from iterating the cubic twice.
Our method depends on using the computer
and a symbolic algebra package to find and solve certain modular
equations.
gives rise to a p-th order iteration. For p=4 we obtain a quartic iteration
due to the Borweins that does not come from the alpha-function.
For p=3 we obtain a cubic iteration
due to the Borweins that does not come from the alpha-function.
For p=7 we find a septic iteration that is analogous to
the cubic iteration. For p=9 we obtain a nonic (ninth order) iteration
that does not seem to come from iterating the cubic twice.
Our method depends on using the computer
and a symbolic algebra package to find and solve certain modular
equations.