![[Shownotes]](../gif/annotate/sshow-21.gif)
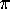 . Although Ramanujan
did not know these algorithms many of the key ingredients
are in his notebooks [13]. The algorithms depend crucially
on the solvable forms of certain modular equations for the theta-functions
due to Ramanujan. In [8] two algorithms are given --
one quartic and one quintic algorithm. In a related paper [5]
a septic algorithm is sketched. In [4] a general method is
given for constructing p-th order algorithms. These algorithms involve defining
a sequence
. Although Ramanujan
did not know these algorithms many of the key ingredients
are in his notebooks [13]. The algorithms depend crucially
on the solvable forms of certain modular equations for the theta-functions
due to Ramanujan. In [8] two algorithms are given --
one quartic and one quintic algorithm. In a related paper [5]
a septic algorithm is sketched. In [4] a general method is
given for constructing p-th order algorithms. These algorithms involve defining
a sequence 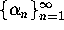 recursively and for which
recursively and for which
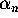 converges to
converges to 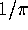 to high order.
In
general, for us, p-th order convergence of a sequence
to high order.
In
general, for us, p-th order convergence of a sequence 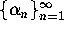 to
to 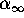 means that
means that 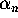 tends to
tends to 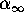 and that
and that

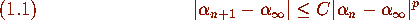 for some constant C>0. The proof of p-th order convergence
depends crucially on identifying
for some constant C>0. The proof of p-th order convergence
depends crucially on identifying 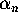 as the value of a certain
function
as the value of a certain
function 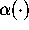 , which can be defined in terms of elliptic
integrals or equivalently in terms of theta-functions.
, which can be defined in terms of elliptic
integrals or equivalently in terms of theta-functions.
Since [8] was first written, Borwein and Borwein [6]
found an amazing cubic algorithm. See also [7]. This algorithm
comes from a certain hypergeometric analog of elliptic integrals that was studied
by Ramanujan. In this paper, we make an attempt to unify some of these results
and find new algorithms. Instead of a fixed function 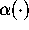 , we define
an infinite family of functions
, we define
an infinite family of functions 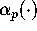 for p>1. Our goal is
to construct for each p, a p-th order iteration which converges to
for p>1. Our goal is
to construct for each p, a p-th order iteration which converges to 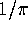 ,
using the function
,
using the function 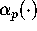 .
.
In Section
2
we briefly describe the Borwein and Borwein
 -function.
In Section
3
we define
-function.
In Section
3
we define 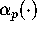 (for each p>1), in terms of
Dedekind's
eta function. We find that
(for each p>1), in terms of
Dedekind's
eta function. We find that 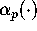 satisfies a nice modular
transformation property, and a nice p-th order modular equation.
In Section
4
we show how the results in Section 3 may be
used to construct p-th order iterations which converge to
satisfies a nice modular
transformation property, and a nice p-th order modular equation.
In Section
4
we show how the results in Section 3 may be
used to construct p-th order iterations which converge to
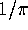 . The method is illustrated with some MAPLE sessions.
In Section
5
we give a brief overview of how our method relates to known quadratic,
cubic and quartic Borwein and Borwein iterations. Details are given how
the cases p=2, 4 relate to the quadratic and quartic algorithms.
In Section
6
we show how the case p=3 gives the Borwein and Borwein cubic
algorithm.
. The method is illustrated with some MAPLE sessions.
In Section
5
we give a brief overview of how our method relates to known quadratic,
cubic and quartic Borwein and Borwein iterations. Details are given how
the cases p=2, 4 relate to the quadratic and quartic algorithms.
In Section
6
we show how the case p=3 gives the Borwein and Borwein cubic
algorithm.
Our main goal in this paper is to somehow mimic the Borwein and
Borwein cubic algorithm and obtain analogous higher order algorithms.
In Section
7
we obtain an explicit solvable septic iteration which converges to 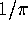 .
In Section
8
we obtain an explicit solvable nonic (ninth order) iteration which
converges to
.
In Section
8
we obtain an explicit solvable nonic (ninth order) iteration which
converges to 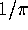 . This nonic iteration does not appear to
come from iterating the cubic twice.
. This nonic iteration does not appear to
come from iterating the cubic twice.
Given the organic nature of this document, we hope, in a later version of this paper, to provide more complete
details and improvements of the septic and nonic algorithms. In a later
version we will also include some mixed order algorithms. For instance,
although the case p=2 leads naturally to a quadratic iteration we may
instead use it to construct a new cubic iteration.