
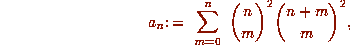 which were introduced in Apéry's proof of the irrationality of
which were introduced in Apéry's proof of the irrationality of 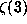 .
At first, a few seemingly surprising congruences were found for these numbers,
but in 1982, Gessel [7] showed that these were
all consequences of the fact that the Apéry numbers satisfy
`Lucas--type' and `Wolstenholme--type' Theorems
(that is
.
At first, a few seemingly surprising congruences were found for these numbers,
but in 1982, Gessel [7] showed that these were
all consequences of the fact that the Apéry numbers satisfy
`Lucas--type' and `Wolstenholme--type' Theorems
(that is 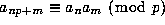 and
and 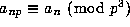 for all
for all 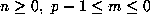 and primes
and primes 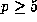 ).
R. McIntosh has asked whether a non--trivial sequence of integers,
satisfying a `Lucas--type' Theorem, can grow slower than
).
R. McIntosh has asked whether a non--trivial sequence of integers,
satisfying a `Lucas--type' Theorem, can grow slower than 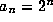 ?
?