![[Shownotes]](../gif/annotate/shide-131.gif)

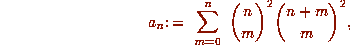 which were introduced in Apéry's proof of the irrationality of
which were introduced in Apéry's proof of the irrationality of 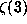 .
At first, a few seemingly surprising congruences were found for these numbers,
but in 1982, Gessel [7] showed that these were
all consequences of the fact that the Apéry numbers satisfy
`Lucas--type' and `Wolstenholme--type' Theorems
(that is
.
At first, a few seemingly surprising congruences were found for these numbers,
but in 1982, Gessel [7] showed that these were
all consequences of the fact that the Apéry numbers satisfy
`Lucas--type' and `Wolstenholme--type' Theorems
(that is 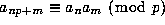 and
and 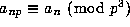 for all
for all 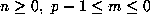 and primes
and primes 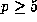 ).
R. McIntosh has asked whether a non--trivial sequence of integers,
satisfying a `Lucas--type' Theorem, can grow slower than
).
R. McIntosh has asked whether a non--trivial sequence of integers,
satisfying a `Lucas--type' Theorem, can grow slower than 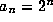 ?
?
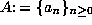 of integers, one
can generalize the notion of factorials and binomial coefficients by taking
of integers, one
can generalize the notion of factorials and binomial coefficients by taking
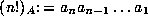 and
and
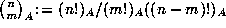 ,
and ask what power of a prime p divides
,
and ask what power of a prime p divides
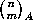 , and also for the value of
, and also for the value of 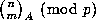 .
The first of these questions is attacked systematically in [12].
A nice example was given by Fray [6], who proved
`Kummer--type' and `Lucas--type' Theorems for the
sequence of `q--binomial coefficients' (where each
.
The first of these questions is attacked systematically in [12].
A nice example was given by Fray [6], who proved
`Kummer--type' and `Lucas--type' Theorems for the
sequence of `q--binomial coefficients' (where each 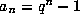 ).
).
There are a number of questions that have received a lot of attention in the literature which do not concern us here. Many require straightforward manipulations of some of the results given here (for instance, how many entries of a given row of Pascal's triangle are not divisible by p), others easy generalizations (for instance to multinomial coefficients --- most results in that area follow immediately from the fact that multinomial coefficients can be expressed as a product of binomial coefficients). People have also investigated the density of entries in Pascal's triangle divisible by any given integer n (and various connections therein to fractals and cellular automata). For these questions, and some others that are not covered here, the reader should look at [2], [19] and [20].