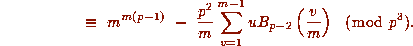Generalization of Morley's Theorem.

Taking n = p-1 in (8.4) gives

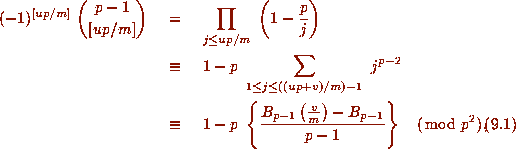which implies (1.15) after summing over each

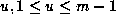, applying (8.1) and then using Fermat's Theorem and the Von Staudt--Clausen Theorem. With a little more work we see that the left side of (1.15) is

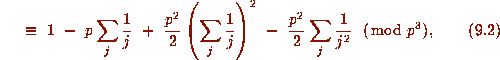where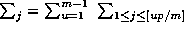

Taking 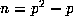and n=p-2 in (8.4), and then using a number of the well--known congruences quoted in section 8 as well as (8.1), we obtain

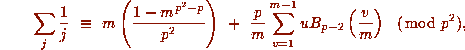and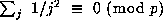

. Substituting these equations into (9.2), and using the fact that

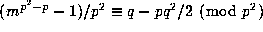for

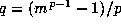, we see that the left side of (1.15) is