![[Shownotes]](../gif/annotate/sshow-91.gif)
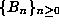 , and the Bernoulli
polynomials,
, and the Bernoulli
polynomials, 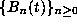 , are defined by the power series
, are defined by the power series

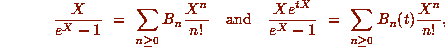 so that
so that 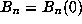 and
and 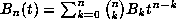 .
Some useful facts, that follow straight from these definitions, are that
each
.
Some useful facts, that follow straight from these definitions, are that
each 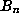 is a rational number,
is a rational number, 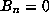 if n is odd and
if n is odd and 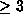 , and
, and

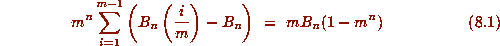 for all integers
for all integers 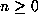 .
In 1840 Clausen and Von Staudt showed that the denominator of
.
In 1840 Clausen and Von Staudt showed that the denominator of 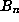 (n even)
is precisely the product of those primes p for which p-1 divides n;
and further that
(n even)
is precisely the product of those primes p for which p-1 divides n;
and further that 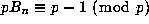 for each such p
(actually one also has
for each such p
(actually one also has 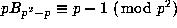 ).
In 1851 Kummer showed that
).
In 1851 Kummer showed that 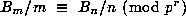 for any even integers m and n, satisfying
for any even integers m and n, satisfying
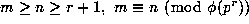 and
and
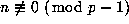 ; and one can use this in showing that
; and one can use this in showing that

 whenever
whenever 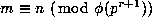 and
and 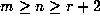 .
Recently Almkvist and Meurman [1] observed that
.
Recently Almkvist and Meurman [1] observed that
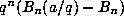 is an integer for any rational number
is an integer for any rational number 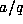 .
.
For any positive integers t and n, we have

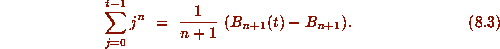 From this, it is easy to deduce analogues for Bernoulli polynomials
of the Von Staudt--Clausen Theorem and of Kummer's congruences.
From this, it is easy to deduce analogues for Bernoulli polynomials
of the Von Staudt--Clausen Theorem and of Kummer's congruences.
We shall assume that
m divides up+v, for given integers 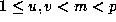 .
By (8.3) we have
.
By (8.3) we have

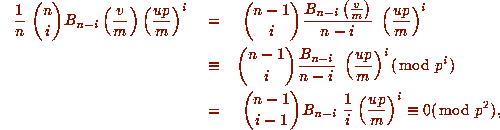 for
for 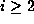 , provided
, provided 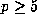 with
with 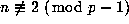 .
Thus, under these conditions,
.
Thus, under these conditions,

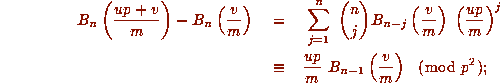 and so, from (8.3), we obtain
and so, from (8.3), we obtain

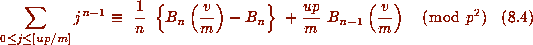 for primes
for primes 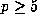 provided
provided 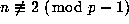 .
.