![[Shownotes]](../gif/annotate/sshow-81.gif)
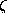 be a primitive p th root of unity and recall that
be a primitive p th root of unity and recall that
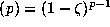 as ideals in Q
as ideals in Q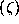 .
Define
.
Define 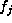 to be the sum on the left side of (1.12) for each j, so that
to be the sum on the left side of (1.12) for each j, so that

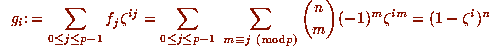 which belongs to the ideal
which belongs to the ideal 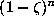 , for
, for 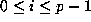 .
Therefore
.
Therefore 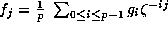 ,
belongs to
,
belongs to 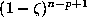 . However, since
each
. However, since
each 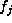 is a rational integer, it must be divisible by
is a rational integer, it must be divisible by 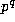 where
where
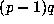 is the smallest multiple of
is the smallest multiple of 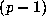 , which is
, which is 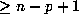 ,
and (1.12) follows immediately.
Proof of (1.13): \
Let d be a quadratic non--residue
,
and (1.12) follows immediately.
Proof of (1.13): \
Let d be a quadratic non--residue 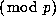 and a, b and n any
positive integers. Define the sequence
and a, b and n any
positive integers. Define the sequence 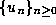 of integers by
of integers by

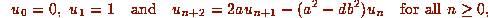 so that, from the binomial theorem,
so that, from the binomial theorem,

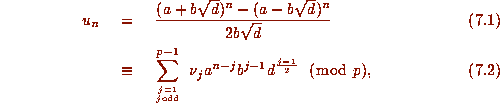 as
as 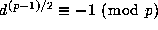 , where
, where 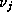 is the sum in (1.13).
is the sum in (1.13).
Now, by Kummer's Theorem,

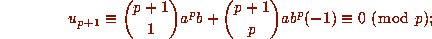 and so, if p+1 divides n then p divides
and so, if p+1 divides n then p divides 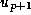 , which divides
, which divides 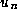 ,
by (7.1). So by selecting a=b=1 and letting d run through all
quadratic non--residues
,
by (7.1). So by selecting a=b=1 and letting d run through all
quadratic non--residues 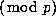 , we have
, we have 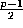 equations
in the
equations
in the 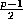 unknowns
unknowns 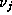 . Therefore each
. Therefore each 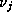 must be
divisible by p as these equations give rise to a Vandermonde matrix
whose determinant is not divisible by p.
must be
divisible by p as these equations give rise to a Vandermonde matrix
whose determinant is not divisible by p.
On the other hand if (1.13) holds for all odd j then
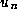 is divisible by p for any admissible choices of a,b and d,
by (7.2). Now fix d and select a and b so that
is divisible by p for any admissible choices of a,b and d,
by (7.2). Now fix d and select a and b so that 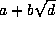 is a
primitive root modulo p in the field Q
is a
primitive root modulo p in the field Q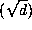 .
Note that
.
Note that
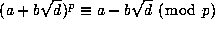 , so that
, so that
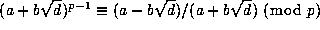 .
By (7.1), we see that
.
By (7.1), we see that
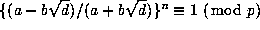 , and so
, and so
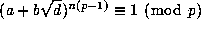 . But
. But 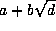 is a
primitive root modulo p and so
is a
primitive root modulo p and so 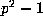 divides
divides 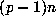 , giving
that p+1 divides n.
, giving
that p+1 divides n.