![[Shownotes]](../gif/annotate/shide-71.gif)
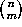 :
Start by noting that
:
Start by noting that 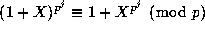 as
each
as
each 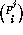 is divisible by p, by Kummer's Theorem, unless
i=0 or
is divisible by p, by Kummer's Theorem, unless
i=0 or 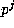 (this is sometimes referred to as ` The Children's Binomial
Theorem'). Therefore, writing n in base p, we have
(this is sometimes referred to as ` The Children's Binomial
Theorem'). Therefore, writing n in base p, we have

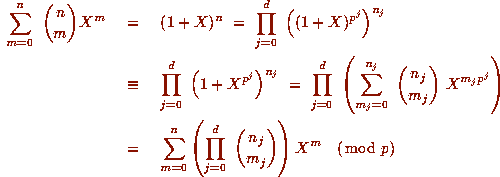 and the result follows.
and the result follows.
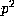 , and arbitrary prime powers, but the details become much more
complicated than in the proof given in section 2. We may also generalize
this method to evaluate, modulo p, the coefficients of powers of any
given polynomial:
, and arbitrary prime powers, but the details become much more
complicated than in the proof given in section 2. We may also generalize
this method to evaluate, modulo p, the coefficients of powers of any
given polynomial:
Given a polynomial 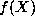 of degree d, with integer coefficients,
we will define
of degree d, with integer coefficients,
we will define 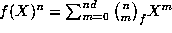 , and let
, and let
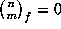 if m<0 or m>nd
(note that
if m<0 or m>nd
(note that 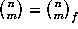 when
when 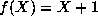 ). Clearly
). Clearly
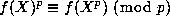 using Fermat's Theorem, and so
using Fermat's Theorem, and so

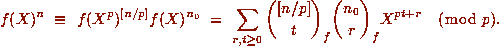 Given m, let
Given m, let 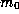 be the least non-negative residue of
be the least non-negative residue of 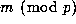 .
Therefore if m = pt+r then r must be of the form
.
Therefore if m = pt+r then r must be of the form 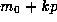 with
with
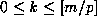 . Thus we obtain the following generalization of (1.1):
. Thus we obtain the following generalization of (1.1):

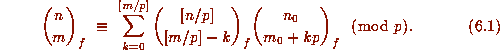 We use a similar approach in the
We use a similar approach in the
Proof of (1.11): By induction on n: For 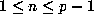 we must have n=k and the only possible value of m in the sum is j,
so that the result is trivial. Now assume that
we must have n=k and the only possible value of m in the sum is j,
so that the result is trivial. Now assume that 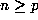 , and write
m and n in base p. Then
, and write
m and n in base p. Then

 for each m in the sum in (1.11), as
for each m in the sum in (1.11), as 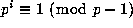 for each i.
Thus, by Lucas' Theorem, the sum in (1.11) is congruent to
for each i.
Thus, by Lucas' Theorem, the sum in (1.11) is congruent to

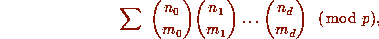 where the sum is over all
where the sum is over all 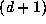 --tuples of integers
--tuples of integers 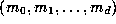 satisfying (6.2) and not all zero. This
is exactly the sum of the coefficients of
satisfying (6.2) and not all zero. This
is exactly the sum of the coefficients of
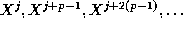 in
in
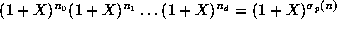 ,
which equals
,
which equals

 (1.11) then follows from the induction hypothesis as
(1.11) then follows from the induction hypothesis as
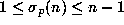 and
and 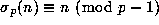 .
.