help

annotate

Contents Next: Congruences modulo powers Up: Arithmetic Properties of Binomial Previous: Generalization of Morley's

Some useful p--adic numbers.

In section 11 we will apply the results from this section to binomial coefficients. We start by proving

Proposition 3. If x is divisible by prime p then

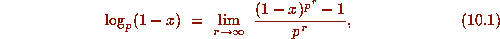where the limit is taken p--adically.

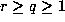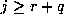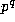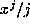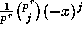Proof: Suppose that . If then divides the numerator of both and . If 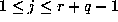and r is sufficiently large then

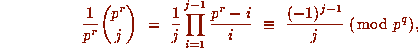so that

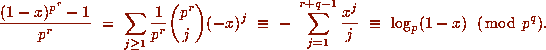Therefore, letting

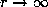and then

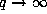, we obtain (10.1).

For each , define

where the limit here is taken p-adically: Note that this limit exists and is well defined by (8.2); moreover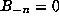

for all odd n. (Using Theorem 5.11 of [21], one can also show that

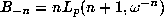, where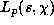

is the p--adic L--function, and

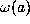is that p--adic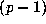

st root of unity for which

.)

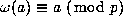Our main result of this section is

Proposition 4. For any integer x we have

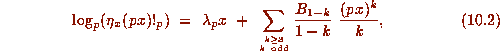where 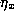(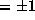) is chosen so that 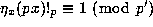, and

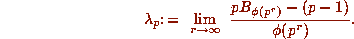
Remark: Note that 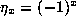if , and 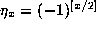if p=2.

(Using Theorem 5.11 of [21], one can also show that

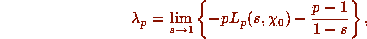where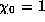

: note that

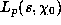has a pole at s=1.)

Proof: As 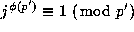whenever p does not divide j, we have

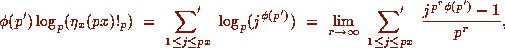by Proposition 3. Now, fix

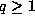and take

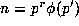with r large in (8.3), so that

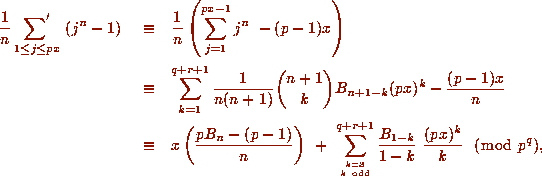for all sufficiently large r, as

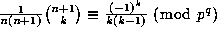for those k in the sum. Therefore, letting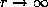

and then

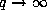, we obtain (10.2).