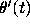, after the balancing transformation.
Theorem 4.7.5 of [4, p. 188] asserts that if 
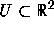is a
narrowing antifunnel for the differential equation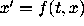 
, and if
there is a function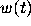 
such that
,
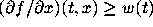in U,
and such that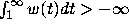 
, then there is a unique
solution remaining in U as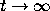 
.
Applied to equation (12), we find
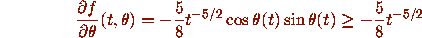for t > 0, so with 
,
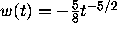the uniqueness criterion is satisfied. This shows that there is a unique
solution remaining in each antifunnel.
Annotation Form Interface