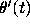, after the balancing transformation.
Theorem 4.7.5 of [4, p. 188] asserts that if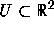 
is a
narrowing antifunnel for the differential equation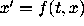 
, and if
there is a function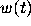 
such that
,
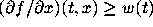in U,
and such that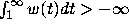 
, then there is a unique
solution remaining in U as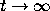 
.
Applied to equation (12), we find
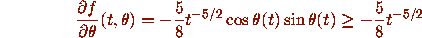for t > 0, so with 
,
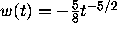the uniqueness criterion is satisfied. This shows that there is a unique
solution remaining in each antifunnel.
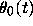of equation (12)
does stay in one of these antifunnels, let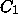 
and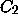 
be defined respectively by the properties
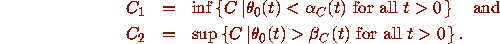Conceivably 
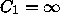or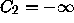 
, but certainly 
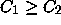, and
we will be done if we can show that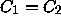 
.
In Figure 
we redraw Figure using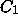 
and 
.
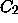If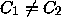 
, choose C with 
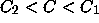; the unique solution
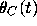lying in the antifunnel defined by 
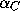and
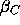must be either above 
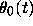or beneath it, because
solutions cannot intersect. If it is above,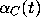 
is also above,
contradicting the definition of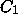 
; if it is beneath, then so is
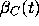, contradiciting the definition of 
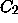. Thus, every solution
is of the form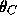 
for some C, and there is a unique such
solution for each C.
Figure 13: Fences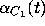 
and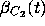 
associated with a solution 
.
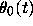![[Annotate]](/organics/icons/sannotate.gif){kind=icon}
![[Shownotes]](../gif/annotate/shide-191.gif)