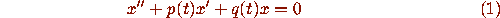
John H. Hubbard - Jean Marie McDill - Anne Noonburg - Beverly H. West
May 1994
Second order linear equations with nonconstant coefficients are a central topic in differential equations. Courses on ``methods of mathematical physics'' or ``special functions'' are largely the study of such equations: Legendre's equation, Bessel's equation, Airy's equation, the hypergeometric equation and Hermite's equation, to name a few. When they are discussed in differential equations courses, the treatment is often reduced to solving
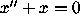yields power
series solutions that represent sine and cosine functions,
but nothing could be less obvious from the series alone than the
fact that they represent periodic functions.
In this paper we will show how to use fences and funnels
to study the asymptotic behavior of solutions to equation (1).
These geometric methods, described briefly in Appendix A, in [3] and more
fully in the book [4], will give a great deal of qualitative and
quantitative information about the solutions without ever requiring a
formula for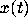 
.
A priori, fence methods are restricted to first-order equations in one variable. But there are two classical methods, due to Riccati and Prüfer [2], [5], that associate a first order nonlinear equation to a second-order homogeneous linear equation. These transformations are easier to understand for systems of first-order linear equations
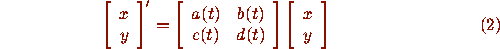
rather than for the second-order equation (1).
A solution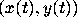 
of (2) is a parametrized curve in the phase
plane (the xy-plane in Figure 1).
The Riccati transformation
describes the evolution of the slope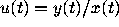 
of the line
through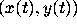 
and the origin, whereas the Prüfer transformation
describes the evolution of the polar angle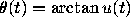 
.
The obvious way of transforming equation (1) into a system
(2) is to set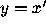 
, leading to the system
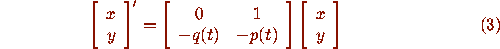
When the solutions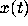 
of (1) are eventually monotone, we can expect
that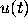 
will have a limit as 
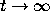, so that the Riccati
equation should be amenable to analysis. When the solutions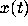 
of (1) are oscillatory, as in
Figure 1, leading to
parametrized curves in the xy-plane turning around the origin, the
slope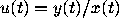 
varies from 
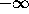to
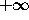infinitely often, and the polar angle given by the Prüfer
transformation is usually much easier to study.
But even the Prüfer transformation can be difficult to analyze if equation (1) is transformed into equation (2) in the obvious way. We will show that there is often a more judicious choice of a second variable
for the Airy equation.