![[Shownotes]](../gif/annotate/sshow-151.gif)
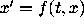 , a time-dependent differential equation in dimension 1,
and
, a time-dependent differential equation in dimension 1,
and 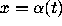 , a curve , defined for a<t<b. Then
, a curve , defined for a<t<b. Then 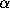 is called
a lower fence if
is called
a lower fence if 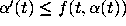 and an upper fence
if
and an upper fence
if 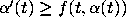 . The drawings corresponding to such curves
are represented in Figure 10.
As the picture suggests, a solution that
starts above a lower fence cannot cross it, and similarily a solution
that starts below an upper fence cannot cross it.
. The drawings corresponding to such curves
are represented in Figure 10.
As the picture suggests, a solution that
starts above a lower fence cannot cross it, and similarily a solution
that starts below an upper fence cannot cross it.


Figure 10: Example of upper and lower fences

There are two important observations about fences: (1) Almost any curve is a fence of some sort, at least in appropriate regions; and (2) you do not need to solve the differential equation to check whether a curve is a fence.
Example.
Does the equation 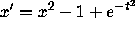 have any monotone increasing
solutions? (This problem is important when tring to understand the
lowest eigenfunction for certain Schrodinger equations.)
have any monotone increasing
solutions? (This problem is important when tring to understand the
lowest eigenfunction for certain Schrodinger equations.)
Solution.
As Figure 11 shows, some solutions increase until they hit
the curve 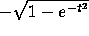 , then decrease to become asymptotic to
x=-1. Are any "fenced away" from the line x=-1? Yes: The curve
, then decrease to become asymptotic to
x=-1. Are any "fenced away" from the line x=-1? Yes: The curve
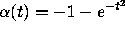 is an upper fence when t>2, since
is an upper fence when t>2, since
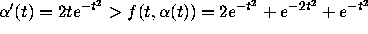 when t>2. Thus all solutions that pass through points
when t>2. Thus all solutions that pass through points 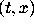 with t>2 and
with t>2 and
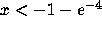 increase monotonically toward the asymptote x=-1, but remain
below this fence. Note that this property is pretty delicate:
there are no such solutions for
increase monotonically toward the asymptote x=-1, but remain
below this fence. Note that this property is pretty delicate:
there are no such solutions for 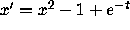 .
.


Figure 11: Monotone increasing solutions of 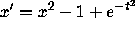

Fences are especially interesting when two are disjoint and close together. This can happen in two ways; If the upper fence is above the lower fence, together they form a funnel; if below it, they form an antifunnel (Figure 12). As the drawing suggests, once a solution enters a funnel, it can never leave it. Especially when the boundaries of a funnel are close together, this can allow a very precise description of the ultimate fate of the whole classes of solutions.


Figure 12: Example of funnels and antifunnels.

Example.
Show that all solutions
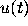 of
of 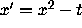 (sketched in Figure 13)
with
(sketched in Figure 13)
with 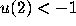 satisfy
satisfy 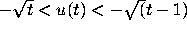 for
sufficiently large t.
for
sufficiently large t.


Figure 13: Solutions of 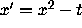 with a funnel and antifunnel
with a funnel and antifunnel

Solution.
The curves 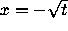 and
and 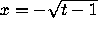 are isoclines of
slope 0 and -1 respectively. The former is a lower fence, and the latter
an upper fence when
are isoclines of
slope 0 and -1 respectively. The former is a lower fence, and the latter
an upper fence when  .
Superimposing these curves over the solution curves in Figure 13,
we see that any solution in the region x<-1, t>2 will enter this funnel
(compare to Figure 9).
.
Superimposing these curves over the solution curves in Figure 13,
we see that any solution in the region x<-1, t>2 will enter this funnel
(compare to Figure 9).
Even more interesting are the antifunnels. A first result is that in every
antifunnel, there is at least one solution. Often there is exactly one
solution, for instance if the antifunnel narrows and
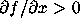 in the
antifunnel. Then you can characterize a particular solution by its
long-term behavior. Often this behavior is exceptional, separating
packages of solutions that all behave in the same way. In most examples
of real interest, this is the most important information we can hope for.
It often answers such questions as: What amount of hunting will lead to
the extinction of a species? What amount of heat will make the boiler
explode?
in the
antifunnel. Then you can characterize a particular solution by its
long-term behavior. Often this behavior is exceptional, separating
packages of solutions that all behave in the same way. In most examples
of real interest, this is the most important information we can hope for.
It often answers such questions as: What amount of hunting will lead to
the extinction of a species? What amount of heat will make the boiler
explode?
Example.
Show that the differential equation
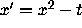 of
Figure 13 has exactly one solution asymptotic to
of
Figure 13 has exactly one solution asymptotic to
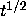 as
as  .
.
Solution.
We superimpose on the graph of solutions of
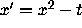 isoclines of slopes 0 and 1 in Figure 13),
and use portions as fences to define an antifunnel. The isoclines
isoclines of slopes 0 and 1 in Figure 13),
and use portions as fences to define an antifunnel. The isoclines
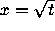 and
and 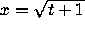 are an upper and a lower fence,
respectively, for
are an upper and a lower fence,
respectively, for 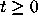 .
Thus, the region between them is a narrowing antifunnel. Since
.
Thus, the region between them is a narrowing antifunnel. Since
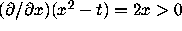 there, the uniqueness conclusion follows.
there, the uniqueness conclusion follows.
Students have no conceptual difficulties with fences, funnels, and antifunnels. On the other hand, the algebraic manipulation of inequalities needed to use them effectively gives many students a lot of trouble. For the qualtitative analysis of differential equations, mastery of inequalities becomes a fundumental skill. Identifying funnels and antifunnels furnishes an endless collection of motivated exercises.