![[Shownotes]](../gif/annotate/sshow-171.gif)

 we will now see how to choose a second variable
we will now see how to choose a second variable

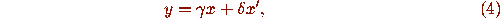 so that Conditions I and II are satisfied. We first need to find the
system of first-order equations satisfied by
x and y; this is old-fashioned computation, but not difficult. The
first equation simply comes from solving (4) for
so that Conditions I and II are satisfied. We first need to find the
system of first-order equations satisfied by
x and y; this is old-fashioned computation, but not difficult. The
first equation simply comes from solving (4) for 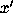 to give
to give

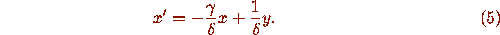
For the second system equation we differentiate (4), use the
differential equation (1) to replace 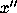 , and use equation
(5) to replace
, and use equation
(5) to replace 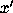 :
:

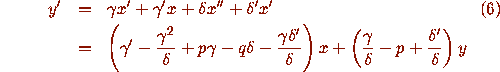
For the Airy equation, with p=0 and q=t, this gives

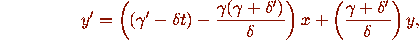 and the system of equations (2) becomes
and the system of equations (2) becomes

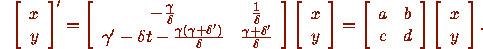
We now choose 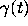 and
and 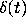 so as to satisfy our two
conditions. The simplest choice for
so as to satisfy our two
conditions. The simplest choice for 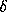 is
is 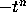 for an
appropriate n (where the negative sign makes the determinant of the
resulting matrix positive). Condition I then implies
for an
appropriate n (where the negative sign makes the determinant of the
resulting matrix positive). Condition I then implies

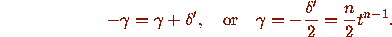
To satisfy Condition II, we need to ensure that

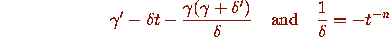 decay at the same rate as
decay at the same rate as  . The first quantity reduces
to
. The first quantity reduces
to

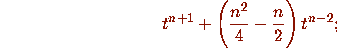 if this is to decay at the same rate as
if this is to decay at the same rate as 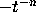 , its largest power
n+1 must be equal to -n, which implies that
, its largest power
n+1 must be equal to -n, which implies that 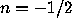 .
This gives
.
This gives

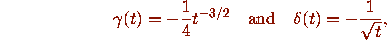 as announced in equation (10).
as announced in equation (10).
Exercise.Show that the variable
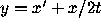 is a balancing variable for the Bessel equation
is a balancing variable for the Bessel equation

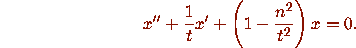 Exercise.Find a balancing variable for the equation
Exercise.Find a balancing variable for the equation
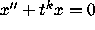 for any k>0, and deduce the asymptotic behavior of
solutions as
for any k>0, and deduce the asymptotic behavior of
solutions as 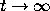 .
.