![[Shownotes]](../gif/annotate/sshow-41.gif)
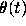 after balancing.
Up:A New Look at
Previous: Analyzing
after balancing.
Up:A New Look at
Previous: Analyzing 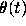 for the
for the
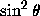 and
and 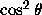 are not of the same
order of magnitude in t, as
are not of the same
order of magnitude in t, as 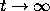 . A better choice of the
second variable y when passing from the second-order equation (1) to
an associated linear system (2) will remedy this.
In general, equation (6) will be easier to analyze if the following two
conditions are satisfied:
. A better choice of the
second variable y when passing from the second-order equation (1) to
an associated linear system (2) will remedy this.
In general, equation (6) will be easier to analyze if the following two
conditions are satisfied:

Although 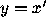 is the usual choice of a second variable when going from
a second-order equation to a first-order system, it is perfectly
permissible to let y be any linear combination of x and
is the usual choice of a second variable when going from
a second-order equation to a first-order system, it is perfectly
permissible to let y be any linear combination of x and 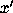 :
:
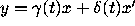 . If we can choose the coefficient functions
. If we can choose the coefficient functions
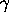 and
and 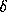 so that C
onditions I and II are satisfied, we will
call the resulting y a balancing variable.
so that C
onditions I and II are satisfied, we will
call the resulting y a balancing variable.
For the Airy equation, a balancing variable is found to be

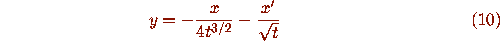 and system (2) becomes
and system (2) becomes

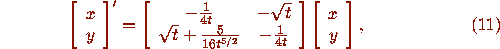
We will explain in Appendix B how (10) and (11) are found, and how to
find balancing variables for other equations. An interesting exercise for
the student is to check that the system (11) is indeed equivalent to the
second-order Airy equation 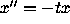 .
.
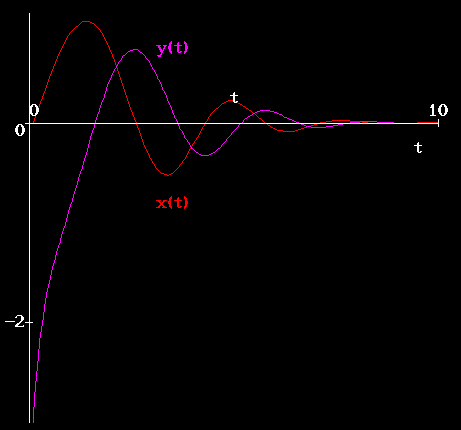
When we look at the graphical results (Figure 3), we can see that the trajectory in the phase plane for this system is more ``circular'' (i.e., x and y are ``balanced''), than in Figure 1.


Figure 3: Graphs of solution to balanced system (11), with 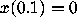 and
and 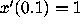 .
.
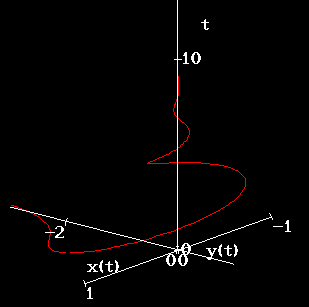
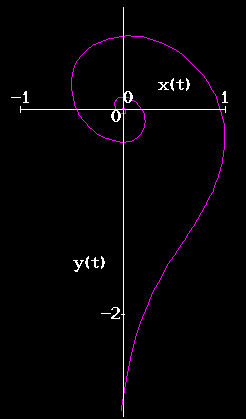
This is reflected in the resulting equation (6) for 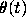 :
:




Figure 4: Trajectories for equation for 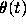 , after balancing.
, after balancing.
 after balancing.
Up:A New Look at
Previous: Analyzing
after balancing.
Up:A New Look at
Previous: Analyzing  for the
for the