The Airy Equation

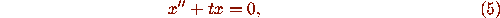
one example of a second-order equation like (1). (Producing such plots do not require advanced numerical software; they can be done with a simple graphing calculator.)

  
Figure 1: Graphs of solutions to the Airy equation with 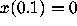and .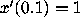

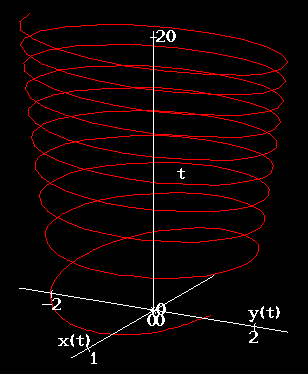
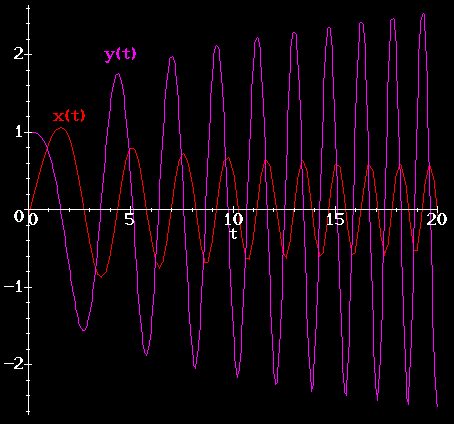
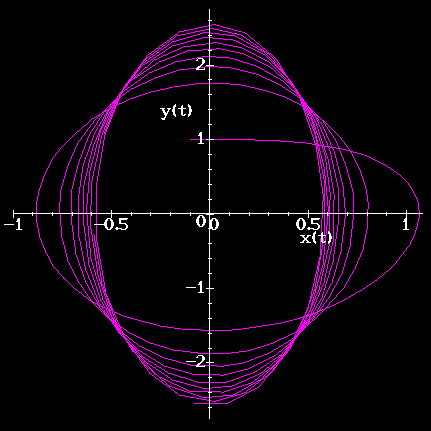
The graphs in Figure 1 raises several questions about the long-term behavior of such solutions. In fact, the analytical solution of Airy's equation using Bessel functions (via Maple or Mathematica) gives students no further insight into the actual behavior of the solutions than the original differential equation, unless they happen to know something about Bessel functions and 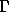functions.

Physically, Airy's equation can be thought of as modeling a spring, vibrating with no damping but with increasing spring constant t > 0 (e.g., a spring vibrating in a rapidly chilling room). As 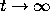, would you expect the spring to vibrate more rapidly, with decreasing amplitude, as the xt graph in Figure 1 indicates? Examining Figure 1 might lead students to ask the following questions.

Question 1. What is the behavior of the solutions to Airy's equation as t becomes large? Does the amplitude of the vibrations decrease toward zero with time, or is it heading toward some other limiting amplitude? The spacing of the zeros of the function appears to be decreasing with time, i.e., the oscillations become more compressed. Does the spacing between adjacent zeros approach 0 as ?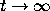

Question 2. What types of solutions exist for t < 0? What happens for negative t that is not pictured in Figure 1? Are there any oscillatory solutions? Are any solutions bounded? For a given value of 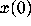, is there a unique bounded solution? The asymptotic behavior of the solutions of Airy's equation is known [1], but the methods traditionally used require some serious complex analysis and are usually reserved for a graduate course in applied mathematics.