Analyzing r'/r.

help

annotate

Contents Next: What Happens for Up: The balancing transformation. Previous: Analyzing

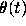after balancing.

Analyzing r'/r.

There is still the question of the amplitude of

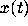. With the values of a, b, c and d from equation (11) inserted into equation (7),

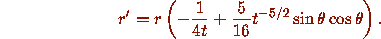Since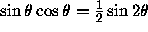

lies between

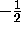and

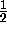, it follows that

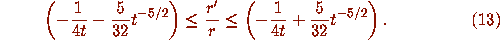Integrating this inequality shows that

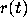behaves like

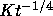for some constant K; that is, the amplitude of

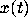decreases to 0 slowly, like

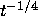, as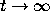

. Combining our results for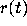

and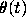

we can now say with certainty that the solutions of Airy's equation behave like

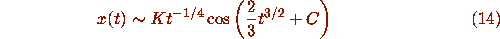as

.

help

annotate

Contents Next: What Happens for Up: The balancing transformation. Previous: Analyzing

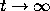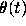after balancing.