![[Shownotes]](../gif/annotate/sshow-111.gif)
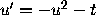 with
with 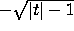 and
and
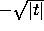 as
as 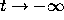 .
.
That is, for all t less than some negative constant 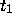 . This inequality can
be integrated from t to
. This inequality can
be integrated from t to 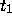 ; an argument identical to the one above
then shows that
; an argument identical to the one above
then shows that

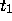 is the time when
is the time when 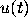 enters the funnel. It can be shown
[4, .6] that the solutions with
enters the funnel. It can be shown
[4, .6] that the solutions with 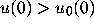 (more generally all
solutions lying above the curve
(more generally all
solutions lying above the curve 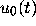 in the left half-plane) become
unbounded at a finite time
in the left half-plane) become
unbounded at a finite time 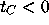 ; such solutions
; such solutions 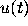 are defined
only for
are defined
only for 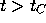 .
.
Exercise. Use similar techniques to identify the
behavior of solutions to 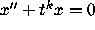 , for any k>0.
, for any k>0.