Dear Professor Mays!
Thank you very much for your letter and for your interest in the function
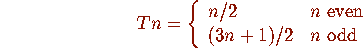which I investigated (in addition to various other number theoretic
functions) almost 50 years ago. In 1929 I attended classes
of E. Land and lectures in number theory given by Lettenmeyer,
both in Göttingen, and in 1930 I attened classes given by
O. Perron in Munich and Isai Schur in Berlin. I found it interesting to
sketch the graphs of number theoretic functions 
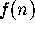by drawing
an arrow from n to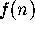 
, or more simply, by writing 
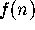under n.
(In this way) one can find various concepts which are well known in the
theory of digraphs such as trees, cycles, bifurcation, etc.
I don't know who the first person was to make these connections to
graph theory; I, however, have seen neither in lectures nor in
published form this type of representation of number theoretic functions.
I enjoy observing the various patterns, and I computed the graphs (at the time
of these investigations) of many interesting number theoretic functions
for values of n up to about 100. I examined the example that I mention
above in this way too, which I rendered in the essentially equivalent form
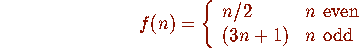
The unessential difference is for n odd:
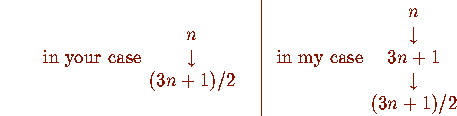
In lectures that I have held as well as at the occasional conference I introduced this example and stated the problem: does the number n=80 belong to a cycle or not? At that time I only had a small table top calculator at my disposal and as far as I could calculate n=80 resulted in no cycle and I could not answer the question. Meanwhile I have spoken with several number theorists about this problem but as far as I know no answer has yet been given to this problem. Partial results have been obtained. Professor Garner provided a partial result, a copy of which I am enclosing. Further I am including a copy of a small section of my graphs. If you know of a solution I would be very thankful to hear from you.
I am sorry that I have written this letter in German. I hope you can find someone who can translate this letter for you.
Sincerely, your humble servant
P.S. If it is not too bold, might I mention that Prof. H. Hasse called the above problem "The Collatz' problem".