![[Shownotes]](../gif/annotate/sshow-111.gif)
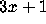 problem can be generalized by considering other functions
problem can be generalized by considering other functions
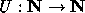 defined on the natural numbers
defined on the natural numbers 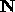 that are
similar to the function T.
The functions I consider to be similar to the function T
are the periodically linear functions, which are those
functions U for which there is a finite modulus d such that the
function U when restricted to any congruence class
that are
similar to the function T.
The functions I consider to be similar to the function T
are the periodically linear functions, which are those
functions U for which there is a finite modulus d such that the
function U when restricted to any congruence class
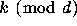 is linear.
Some reasons to study generalizations of the
is linear.
Some reasons to study generalizations of the 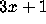 problem are that
they may uncover new phenomena, they can indicate the limits of
validity of known results, and they can lead to simpler,
more revealing proofs.
Here I discuss three directions of generalizations of the
problem are that
they may uncover new phenomena, they can indicate the limits of
validity of known results, and they can lead to simpler,
more revealing proofs.
Here I discuss three directions of generalizations of the
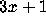 problem.
These deal with algorithmic decidability questions,
with the existence of stopping times for almost all integers, and with the
fractional parts of
problem.
These deal with algorithmic decidability questions,
with the existence of stopping times for almost all integers, and with the
fractional parts of 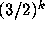 .
.