![[Shownotes]](../gif/annotate/sshow-141.gif)
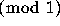 of the sequence
of the sequence 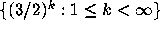 have uncovered oblique
connections with ergodic-theoretic aspects of a generalization of the
3x+1 problem.
It is conjectured that the sequence
have uncovered oblique
connections with ergodic-theoretic aspects of a generalization of the
3x+1 problem.
It is conjectured that the sequence 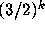 is uniformly distributed
is uniformly distributed
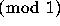 .
.
(This conjecture seems intractable at present.)
One approach to this problem is to determine what kinds of 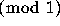 distributions can occur for sequences
distributions can occur for sequences 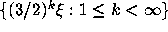 ,
where
,
where 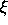 is a fixed real number.
In this vein K. Mahler [49] considered the problem of whether or
not there exist real numbers
is a fixed real number.
In this vein K. Mahler [49] considered the problem of whether or
not there exist real numbers 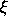 , which he called
Z-numbers,
having the property that
, which he called
Z-numbers,
having the property that

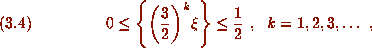 where
where 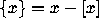 is the fractional part of x.
He showed that the set of Z-numbers is countable, by showing that there
is at most one Z-number in each interval
is the fractional part of x.
He showed that the set of Z-numbers is countable, by showing that there
is at most one Z-number in each interval
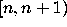 , for
, for 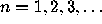 .
He went on to show that a necessary condition for the existence of a Z-number
in the interval
.
He went on to show that a necessary condition for the existence of a Z-number
in the interval 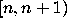 is that the trajectory
is that the trajectory
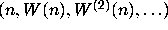 of n produced by the
periodically linear function
of n produced by the
periodically linear function

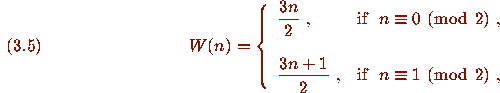 satisfy
satisfy

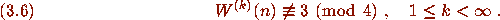 Mahler concluded from this that is unlikely that any Z-numbers exist.
This is supported by the following heuristic argument.
The function W may be interpreted as acting on the 2-adic
integers by (3.5), and it has properties
exactly analogous to the properties of T given by Theorem K.
In particular, for almost all 2-adic integers
Mahler concluded from this that is unlikely that any Z-numbers exist.
This is supported by the following heuristic argument.
The function W may be interpreted as acting on the 2-adic
integers by (3.5), and it has properties
exactly analogous to the properties of T given by Theorem K.
In particular, for almost all 2-adic integers 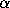 the sequence of
iterates
the sequence of
iterates 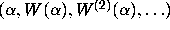 has infinitely many values k with
has infinitely many values k with 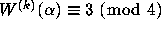 .
Thus if a given
.
Thus if a given 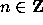 behaves like almost all 2-adic integers
behaves like almost all 2-adic integers
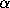 , then (3.6) will not hold for n.
Note that it is possible that all the trajectories
, then (3.6) will not hold for n.
Note that it is possible that all the trajectories
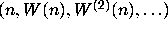 for
for 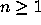 are uniformly
distributed
are uniformly
distributed 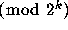 for allk,
unlike the behavior of the function
for allk,
unlike the behavior of the function 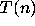 .
.
In passing, I note that the possible distributions 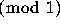 of
of
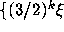 ;
;
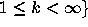 for real
for real 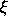 have an intricate structure
(see G. Choquet [16]--[22]
and A. D. Pollington [57], [58]).
In particular, Pollington [58] proves that there are
uncountably many real numbers
have an intricate structure
(see G. Choquet [16]--[22]
and A. D. Pollington [57], [58]).
In particular, Pollington [58] proves that there are
uncountably many real numbers 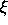 such that
such that

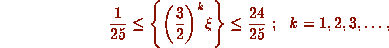 in contrast to the at most countable number of solutions
in contrast to the at most countable number of solutions
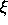 of (3.4).
of (3.4).