

Contents
Next: References
Up: No Title
Previous: Fractional parts of.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/sshow-151.gif)
Is the 3x+1 problem intractably hard?
The difficulty of settling the 3x+1 problem seems connected to the
fact that it is a deterministic process that simulates ``random''
behavior.
We face this dilemma:
On the one hand, to the extent that the problem has structure,
we can analyze it ---
yet it is precisely this structure that seems to prevent us from proving
that it behaves ``randomly.''
On the other hand, to the extent that the problem is structureless
and ``random,''
we have nothing to analyze and consequently cannot rigorously prove anything.
Of course there remains the possibility that someone will find some hidden
regularity in the 3x+1 problem that allows some of the conjectures about it to be settled.
The existing general methods in number theory and ergodic theory do not
seem to touch the 3x+1 problem; in this sense it
seems intractable at present.
Indeed all the conjectures made in this paper seem currently to be out of
reach if they are true; I think there is more chance of
disproving those that are false.
If the 3x+1 problem is intractable, why should one bother to study it?
One answer is provided by the following aphorism: ``No problem is so
intractable that something interesting cannot be said about it.''
Study of the 3x+1 problem has uncovered a number of interesting phenomena;
I believe further study of it may be rewarded by the discovery of
other new phenomena.
It also serves as a benchmark to measure the progress of general
mathematical theories.
For example,
future developments in solving exponential Diophantine equations may lead to the
resolution of the Finite Cycles Conjecture.
If all the conjectures made in this paper are intractable, where would one
begin to do research on this deceptively simple problem?
As a guide to doing research, I ask questions.
Here are a few that occur to me:
For the 3x+1 problem, what restrictions are there on the growth in size
of members of a divergent trajectory assuming that one exists?
What interesting properties does the function  have?
Is there some direct characterization of
have?
Is there some direct characterization of  other than the recursive definition (2.33)?
other than the recursive definition (2.33)?


Contents
Next: References
Up: No Title
Previous: Fractional parts of.
![[Shownotes]](../gif/annotate/sshow-151.gif)
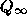 have?
Is there some direct characterization of
have?
Is there some direct characterization of 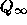 other than the recursive definition (2.33)?
other than the recursive definition (2.33)?