Contents Next: The Beginning of Up:The Search for a Previous: Prologue

The History of the Problem

A finite projective plane of ordern, with n > 0, is a collection of

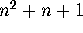lines and

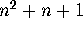points such that

every line contains n+1 points,
every point is on n+1 lines,
any two distinct lines intersect at exactly one point, and
any two distinct points lie on exactly one line.

Figure 1: The finite projective plane of order two

There are several different definitions for a finite projective plane and this set of axioms is chosen to highlight the striking duality of lines and points. One can interchange the words ``line'' and ``point'' in the definition and obtain essentially the same axioms! The attractiveness of these objects is in their simplicity and their reliance on the language of geometry. One is tempted to start drawing lines on paper and may soon discover some simple examples.

The smallest example of a finite projective plane is a triangle, the plane of order one. The smallest non-trivial example is of order 2, as shown in Fig. 1. There are seven points labelled from 1 to 7. There are also seven lines labelled L1 to L7. Six of them are straight lines but L6 is represented by the circle through the points 2, 6, and 7. The reader is invited to verify that the axioms of a finite projective plane are satisfied.

An early reference to a finite projective plane is in the paper by Veblen [32], which studied the axioms for geometry and used the plane of order 2 as an example. Veblen also proved that this plane of order 2 cannot be drawn using only straight lines. In a series of papers [32,33,34], Veblen, Bussey and Wedderburn established the existence of most of the planes of small orders, as well as all four non-isomorphic planes of order 9. One of the orders missing is n = 6.

Figure 2: Two orthogonal latin squares of order four

Figure 3: A Graeco-Latin square of Order 4

In 1938, Bose [4] explained why there is no projective plane of order 6. He related the existence of a finite projective plane of order n to the existence of a hyper-Graeco-Latin square. The term ``Graeco-Latin square'' originated with Euler in 1782. In our modern terminology, they are called orthogonal Latin squares. Let us define them.

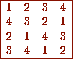
Figure 4: A Latin square orthogonal to those in Fig. 2

A Latin square of order n is an 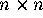matrix satisfying the following properties:

all the entries are integers between 1 and n,
in every row, no entry is repeated, and
in every column, no entry is repeated.

Let

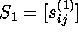and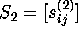

denote two Latin squares of order n. They are said to be orthogonal provided that the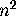

2-samples

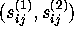for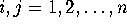

are distinct. A simple way to visualize the definition is to put the second square, slightly shifted, on top of the first square. The resulting n by n array of 2-samples has no repeated entries, and is often referred to as a Graeco-Latin square or an Euler square. Figure 2 contains two examples of Latin squares of order 4. They are orthogonal and the resulting Graeco-Latin square is shown in Fig. 3. Is there a third Latin square orthogonal to both the squares in Fig. 2? Yes, there is one, as shown in Fig. 4. Can one find a fourth? The answer is no. One can easily prove the following theorem [26, p. 80,].

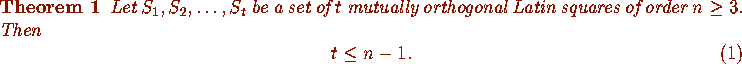
If equality holds in (1), then the orthogonal set is said to be complete. Finally, we are ready to state Bose's result [26, p. 92,].

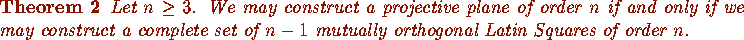
Why does Bose's result explain the non-existence of a projective plane of order 6? It states that such a plane exists if and only if there exists a complete set of 5 mutually orthogonal Latin squares of order 6. The possible existence of even a pair of orthogonal Latin squares of order 6 was a much older problem.

In a 1782 paper [12], Euler started by stating the problem of the 36 officers. This problem asks for an arrangement of 36 officers of 6 ranks and from 6 regiments in a square formation of size 6 by 6. Each vertical and each horizontal line of this formation is to contain one and only one officer of each rank and one and only one officer from each regiment. Euler denoted the 6 regiments by the Latin letters a,b,c,d,e,f and the 6 ranks by the Greek letters 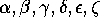. He further remarked that the characteristic of an officer was determined by the two letters, one Latin and the other Greek, and that the problem consists of arranging the 36 combinations of two letters in a square in such manner that every row and every column contains the six Latin as well as the six Greek letters. This was the origin of the term ``Graeco-Latin square''. Euler observed that the first step was to arrange the Latin letters in a square so that no letter was missing either from any row or from any column. He called this square a Latin square. If he had chosen to arrange the Greek letters instead, then we would probably have Graeco squares rather than Latin squares. In any case, if we label both the ranks and the regiments from 1 through 6, then Euler's problem reduces to the construction of a pair of orthogonal Latin squares of order 6.

Euler found no solution to this particular problem. He then conjectured that no solution exists if the order of the square is of the form 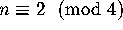. This is the famous Euler's conjecture. The first case n = 2 is trivially impossible. Tarry around 1900 [27] verified by a systematic enumeration that Euler's conjecture holds for n = 6. Since there does not exist even a pair of orthogonal Latin squares, Bose's result implies the non-existence of a projective plane of order 6. Yet, there is something unpleasant about a systematic hand enumeration: it is messy and it is error prone. Mathematicians did find a better explanation in the celebrated Bruck-Ryser theorem [7], which was published in 1949.

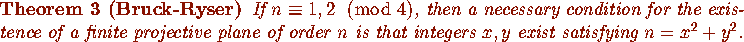
Since 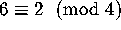and it is not a sum of two integer squares, the Bruck-Ryser theorem implies the non-existence of a projective plane of order 6. How did they prove the theorem? We will not repeat it here, but one of the crucial steps involved the use of an incidence matrix.

Figure 5: An incidence matrix for the plane of order two

The incidence matrix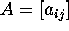 of a projective plane of order n is an 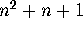by 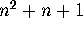matrix where the columns represent the points and the rows represent the lines. The entry 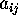is 1 if point j is on line i; otherwise, it is 0. For example, Fig. 5 gives the incidence matrix for the projective plane of order 2. In terms of an incidence matrix, the properties of being a projective plane are translated into:

A has constant row sum n+1,
A has constant column sum n+1,
the inner product of any two distinct rows of A is 1, and
the inner product of any two distinct columns of A is 1.

The conditions on row sums and row inner products can be encapsuled in the following matrix equation:

where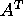

denotes the transpose of the matrix A, I denotes the identity matrix, and J the matrix of all 1's. Every diagonal entry on the right hand side of Eq. (2) is n+1, which implies that the inner product of any row of A with itself is n+1 or, equivalently, its row sum is n+1. Every off-diagonal entry is 1, which is the same as requiring the inner product of any two distinct rows of A to be 1. Ryser also proved that A is a normal matrix [25]; in other words,

Hence, Eq. (2) also implies the conditions regarding column sums and column inner products. The Bruck-Ryser theorem starts from this equation and proves that it implies n is a sum of two integer squares when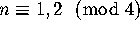

. It is surprising that the Bruck-Ryser theorem has a partial converse [13].

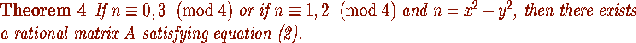Of course, if the matrix A is actually the incidence matrix of a projective plane, then it must have entries which are either 0 or 1. Although this theorem guarantees only a matrix with rational entries, it suggests that the necessary part of the Bruck-Ryser theorem is very close to being also sufficient.

Projective planes are special cases of a class of combinatorial objects called symmetric block designs. We are not going to discuss block designs, except to mention that Chowla and Ryser have generalized the Bruck-Ryser theorem to symmetric block designs [10], which it is now known as the Bruck-Ryser-Chowla theorem. Here again, a partial converse exists, providing more credence to the hope that the conditions in the Bruck-Ryser-Chowla theorem are both necessary and sufficient. This hope is now shattered by the non-existence of the finite projective plane of order 10. Let us return to the history of projective planes. Now that we have a good explanation of the non-existence of a plane of order 6, what is the next unknown case? It is n = 10. Since 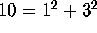, a plane of order 10 would exist if the necessary condition of the Bruck-Ryser theorem is also sufficient. On the other hand, 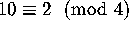, and so, if one believes Euler's conjecture, then it does not exist.

First, Euler's conjecture was shown to be false. In 1959, Bose and Shrikhande [5] constructed a pair of orthogonal Latin squares of order 22. Then Parker [23,24] constructed a pair of orthogonal Latin squares of order 10. Together they showed that Euler's conjecture is false for all orders greater than six [6]. This raised the hope for the existence of a plane of order 10.

History indicated that significant advances were made when one branch of mathematics was shown to be related to a different branch of mathematics. It is not surprising that the beginning of the end of the plane of order 10 occurred when people started studying the binary error-correcting code associated with it.

Contents Next: The Beginning of Up:The Search for a Previous: Prologue