![[Shownotes]](../gif/annotate/sshow-11.gif)

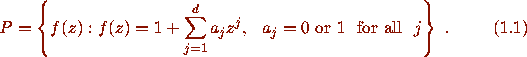
(We exclude polynomials with constant term 0, as their zeros, other than 0, are those of polynomials of lower degree with coefficients 0,1.) Define

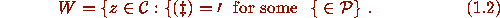 For each degree d, there are
For each degree d, there are 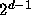 polynomials
polynomials 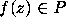 of degree d, and so W is a countable set.
of degree d, and so W is a countable set.
There are few published results about W.
In [8] it was shown that 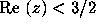 for all
for all 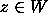 . This was used to prove that if
. This was used to prove that if 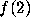 is a prime
for some
is a prime
for some 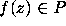 , then
, then 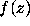 is irreducible over the
rationals.
(For further results relating zeros to irreducibility, see
[12].
It is conjectured that almost all
is irreducible over the
rationals.
(For further results relating zeros to irreducibility, see
[12].
It is conjectured that almost all 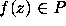 are
irreducible, but this is still open.
This is in contrast to the case of fixed degree polynomials when
the range over which the coefficients are allowed to run
increases.
There it is known that almost all polynomials are not only
irreducible, but also have
are
irreducible, but this is still open.
This is in contrast to the case of fixed degree polynomials when
the range over which the coefficients are allowed to run
increases.
There it is known that almost all polynomials are not only
irreducible, but also have 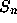 as their Galois group.
For latest results and references on this topic, see
[14].)
as their Galois group.
For latest results and references on this topic, see
[14].)
Our results are best illustrated by pictures of zeros.
Figure 1 shows all zeros of
the
polynomials with
coefficients 0,1 of degrees 12 and less,
and with constant term 1,
except for the negative real zeros that lie are 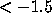 .
We show that W lies
between the curves
.
We show that W lies
between the curves

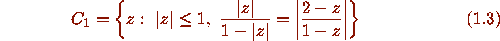 and
and

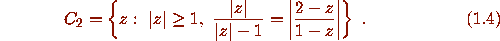 The curve
The curve 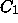 is mapped to
is mapped to 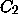 by
by 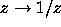 .
This mapping takes W to itself, since if
.
This mapping takes W to itself, since if 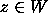 , and z is a root of
, and z is a root of 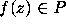 and
and
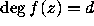 , then
, then 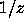 is a root of
is a root of 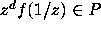 .
We show that all
.
We show that all 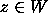 are enclosed strictly between
are enclosed strictly between 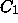 and
and 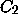 .
>From this it follows that
for all
.
>From this it follows that
for all 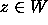 ,
,

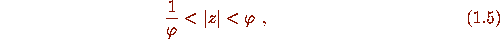 where
where

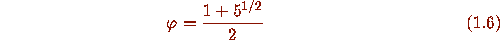 is the ``golden ratio.''
(The bound
is the ``golden ratio.''
(The bound 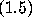 has been proved independently in different contexts by
Flatto, Lagarias, and Poonen [13] and by Solomyak
[16].)
We also show that the line segment
has been proved independently in different contexts by
Flatto, Lagarias, and Poonen [13] and by Solomyak
[16].)
We also show that the line segment 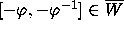 .
However,
.
However, 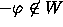 and
and 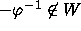 .
Further, there is a constant
.
Further, there is a constant 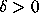 such that if
such that if 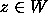 ,
,
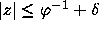 , then
, then 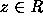 .
Thus the
``spike'' along the negative real axis that is visible
in Fig. 1, connecting curves
.
Thus the
``spike'' along the negative real axis that is visible
in Fig. 1, connecting curves 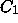 and
and 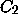 with the exception
of a small gap at -1, is due to zeros.
with the exception
of a small gap at -1, is due to zeros.
Since polynomials in P have nonnegative coefficients,
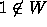 .
However, since
.
However, since 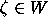 for every root of unity
for every root of unity 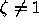 ,
, 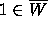 , where
, where 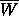 denotes the
closure of W.
We answer a question posed by J. H. Conway and Richard Parker
about the behavior of W near 1 by proving there exist points
denotes the
closure of W.
We answer a question posed by J. H. Conway and Richard Parker
about the behavior of W near 1 by proving there exist points
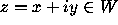 such that
such that 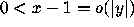 , so that these
points come in tangent to the x-axis.
, so that these
points come in tangent to the x-axis.
Figure 2 shows the zeros of polynomials 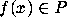 of degree 12
that are close to z=1.
Figure 3
shows zeros of polynomials
of degree 12
that are close to z=1.
Figure 3
shows zeros of polynomials 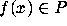 of all degrees
of all degrees
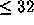 that fall in a certain small region of the complex
plane.
Figures 4,
5, and
6
show pictures of parts of
that fall in a certain small region of the complex
plane.
Figures 4,
5, and
6
show pictures of parts of 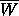 .
The region depicted in
Figure 4is the same as that of
Figure 3.
Section 6 explains how these pictures were created.
.
The region depicted in
Figure 4is the same as that of
Figure 3.
Section 6 explains how these pictures were created.
Theorem 2.1 of
Section 2, which says that W is
contained between 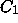 and
and 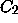 , is not best possible.
The only points of
, is not best possible.
The only points of 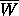 that are in
that are in 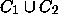 are
1,
are
1, 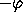 ,
, 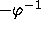 .
In
Section 6 we will show how to obtain more precise bounds for
W.
However, because of the fractal nature of W, there is no simple
description of its shape.
.
In
Section 6 we will show how to obtain more precise bounds for
W.
However, because of the fractal nature of W, there is no simple
description of its shape.
Many features visible in the graphs can be explained (at least
heuristically, and often rigorously) by using known results or
methods.
When one
graphs zeros of any single polynomial with coefficients
0 and 1, most of them are close to the unit circle
|z|=1
and they are equidistributed in angles, so that the first
quadrant, for example, has close to 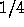 of the total.
This phenomenon is true for all polynomials whose coefficients
do not vary much, as follows from results originating with
Erdös and Turán [11].
For statements and references to general results, see
[4].
of the total.
This phenomenon is true for all polynomials whose coefficients
do not vary much, as follows from results originating with
Erdös and Turán [11].
For statements and references to general results, see
[4].
The expected number of real roots of a random polynomial (which have to be negative for 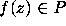 ) grows logarithmically with n,
as was first noted by Kac and Rice (see [4]).
Furthermore, the variance is small.
) grows logarithmically with n,
as was first noted by Kac and Rice (see [4]).
Furthermore, the variance is small.
In Figures 1 and 2, there is a perceptible clustering of zeros. This is a reflection of the ``averaging phenomenon'' for roots of random polynomials [4,15], and again is not special to 0,1 coefficients. The ``average'' of the polynomials of degree n that are in P is

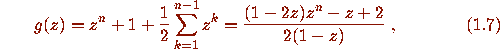 and on average the zeros of
and on average the zeros of 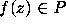 tend to cluster near the zeros of
tend to cluster near the zeros of
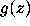 .
.
Figures 1 and 2 show several large ``holes,''
which contain either just one or no zeros.
These holes are usually centered at algebraic integers 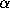 of low degree and small height (i.e.,
algebraic integers
of low degree and small height (i.e.,
algebraic integers 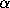 that satisfy
polynomial equations with small integral coefficients).
The most prominent of the holes are at the roots of unity,
such as -1 and i.
As one computes zeros of polynomials
that satisfy
polynomial equations with small integral coefficients).
The most prominent of the holes are at the roots of unity,
such as -1 and i.
As one computes zeros of polynomials 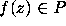 of increasing degrees, the
large holes in Figures 1 and 2 fill up.
However, there are other holes, such as those visible in
Figures
3,
4,
5, and
6
that are free of zeros even when the degree increases.
of increasing degrees, the
large holes in Figures 1 and 2 fill up.
However, there are other holes, such as those visible in
Figures
3,
4,
5, and
6
that are free of zeros even when the degree increases.
We show in
Section 3 that there is an open neighborhood of 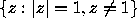 that is in
that is in 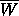 .
In
Section 4 we prove that
.
In
Section 4 we prove that
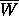 is connected.
The more involved argument in
Section 5 proves that
is connected.
The more involved argument in
Section 5 proves that 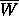 is path connected.
Since the unit circle is contained in
is path connected.
Since the unit circle is contained in 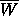 , but
, but 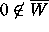 ,
, 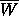 is clearly not simply connected.
Numerical experiments suggest that
is clearly not simply connected.
Numerical experiments suggest that 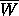 has
``holes'' in it besides the big hole containing 0.
(That is,
has
``holes'' in it besides the big hole containing 0.
(That is, 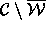 has more than 2 connected components.)
In particular, the disk of radius
has more than 2 connected components.)
In particular, the disk of radius 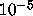 centered at
centered at 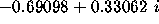 appears to be part of such a hole.
This hole and some neighboring ones are pictured in Figures
5, and
6.
Other, even larger holes, can be seen in Figures
3 and
4.
appears to be part of such a hole.
This hole and some neighboring ones are pictured in Figures
5, and
6.
Other, even larger holes, can be seen in Figures
3 and
4.
W has a fractal appearance that is reminiscent of some of the
Julia sets
[1,10].
In
Section 6
we sketch arguments that explain how this arises.
However, we do not have estimates for such interesting parameters
as the Hausdorff dimension of the boundary of 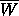 .
.
In contrast to our result that 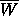 is path connected,
the Mandelbrot set is only known to be
connected, although it is conjectured to be path connected [1,10].
Our methods are simpler than those used to study the connectedness of the Mandelbrot set.
They are similar to the techniques developed for investigating iterated function systems [1].
is path connected,
the Mandelbrot set is only known to be
connected, although it is conjectured to be path connected [1,10].
Our methods are simpler than those used to study the connectedness of the Mandelbrot set.
They are similar to the techniques developed for investigating iterated function systems [1].
Results
similar to those for polynomials with
0,1 coefficients can also be obtained for other families of
polynomials with a small set of possible coefficients.
For example, for
 coefficients,
pictures of zeros are qualitatively similar to those of
0,1 polynomials.
There is symmetry about the imaginary axis as well as the
real axis (corresponding to changing the variable z to -z).
There are two ``spikes''
of zeros along the real axis that fill the intervals
coefficients,
pictures of zeros are qualitatively similar to those of
0,1 polynomials.
There is symmetry about the imaginary axis as well as the
real axis (corresponding to changing the variable z to -z).
There are two ``spikes''
of zeros along the real axis that fill the intervals
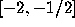 and
and 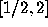 , while there are no other
zeros in
, while there are no other
zeros in 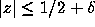 or
or 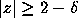 for some
for some 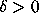 .
For polynomials with cubic roots of unity as coefficients, there are no
``spikes,''
but the zeros still have a fractal appearance.
.
For polynomials with cubic roots of unity as coefficients, there are no
``spikes,''
but the zeros still have a fractal appearance.
The set

 is the set of zeros of power series
is the set of zeros of power series

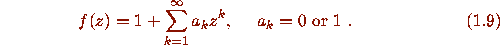 Since
Since 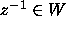 for all
for all 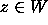 , it is sufficient to study
, it is sufficient to study 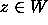 ,
, 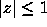 , and in
some ways it is more natural to deal with the above power series.
, and in
some ways it is more natural to deal with the above power series.
Some of our methods and results are similar to those of Thierry
Bousch [5,6], whose work was brought to our attention
by D. Zagier.
The report [5] proves that the closure of the set of
zeros of polynomials with coefficients 0, 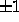 is connected.
The thesis [6] contains, along with a variety of other
results, general methods for studying similar problems.
In the area where our work overlaps [5,6], we obtain a
somewhat stronger result by proving path connectivity.
is connected.
The thesis [6] contains, along with a variety of other
results, general methods for studying similar problems.
In the area where our work overlaps [5,6], we obtain a
somewhat stronger result by proving path connectivity.
Boris Solomyak [16] has studied zeros of power series of
the form 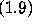 , but with the
, but with the 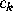 ,
, 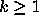 , allowed to
take any real values in the interval
, allowed to
take any real values in the interval 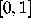 .
He shows that the bound
.
He shows that the bound 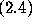 holds there as well, and that
there is a
``spike'' of real zeros along the negative real axis.
However, the zeros of Solomyak's functions are substantially
different from those we investigate.
For example, he shows that segments of the boundary he
investigates have everywhere dense sets of points where a
tangent exists, as well as everywhere dense sets of points with
no tangent.
There are also no holes in Solomyak's set of zeros.
holds there as well, and that
there is a
``spike'' of real zeros along the negative real axis.
However, the zeros of Solomyak's functions are substantially
different from those we investigate.
For example, he shows that segments of the boundary he
investigates have everywhere dense sets of points where a
tangent exists, as well as everywhere dense sets of points with
no tangent.
There are also no holes in Solomyak's set of zeros.
The paper of Brenti, Royle, and Wagner [7] discusses various properties of chromatic polynomials. While it is not directly related to our work, the numerical evidence it presents shows that zeros of chromatic polynomials may also exhibit fractal behavior. This may also be true for the partition function zeros of [3].