![[Shownotes]](../gif/annotate/shide-41.gif)
 , truncated at 500,000 terms gives to forty places
, truncated at 500,000 terms gives to forty places

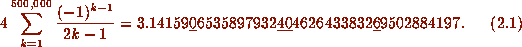
Theorem 1. For integer N divisible by 4 the following asymptotic expansion holds:

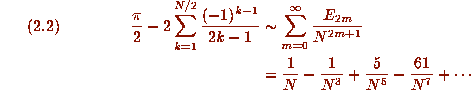 where the coefficients are
the even Euler numbers 1, -1, 5, -61, 1385,
where the coefficients are
the even Euler numbers 1, -1, 5, -61, 1385,  .
.
The Computational Component. The observation 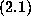 arrived in the
mail from Roy North. After verifying its truth numerically, it was an easy
matter to generate a large number of the ``errors'' to high precision. We
then recognized the sequence of errors in
arrived in the
mail from Roy North. After verifying its truth numerically, it was an easy
matter to generate a large number of the ``errors'' to high precision. We
then recognized the sequence of errors in 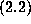 as the Euler numbers ---
with the help of Sloane's `Handbook of Integer Sequences'. The
presumption that
as the Euler numbers ---
with the help of Sloane's `Handbook of Integer Sequences'. The
presumption that 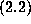 is a form of Euler-Maclaurin summation is now
formally verifiable for any fixed N in Maple. This allowed us to
determine that
is a form of Euler-Maclaurin summation is now
formally verifiable for any fixed N in Maple. This allowed us to
determine that 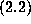 is equivalent to a set of identities between
Bernoulli and Euler numbers that could with effort have been established.
Secure in the knowledge that
is equivalent to a set of identities between
Bernoulli and Euler numbers that could with effort have been established.
Secure in the knowledge that 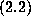 holds it is easier, however, to use the
Boole Summation formula which applies directly to alternating series and
Euler numbers (see [5]).
holds it is easier, however, to use the
Boole Summation formula which applies directly to alternating series and
Euler numbers (see [5]).
This is a good example of a phenomenon which
really does not become apparent without working to reasonably high
precision (who recognizes 2, -2, 10 ?), and which highlights the role
of pattern recognition and hypothesis validation in experimental
mathematics. It was an amusing additional exercise to compute Pi to
5,000 digits from 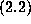 . Indeed, with N = 200,000 and correcting using
the first thousand even Euler numbers, we obtained 5,263 digits of Pi
(plus 12 guard digits).
. Indeed, with N = 200,000 and correcting using
the first thousand even Euler numbers, we obtained 5,263 digits of Pi
(plus 12 guard digits).
2b. The Mathematical Component. The following evaluations are correct to the precision indicated.
Sum 1 (correct to all digits)


where 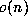 counts the
counts the 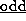 digits in n:
digits in n: 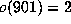 ,
, 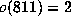 ,
, 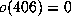 .
.
By comparison
Sum 2 (correct to 30 digits)


where 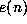 counts the even digits in n.
counts the even digits in n.
Sum 3 (correct to 267 digits)


where  is the greatest integer function:
is the greatest integer function: 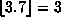 .
.
Sum 4 (correct to in excess of 500 million digits)

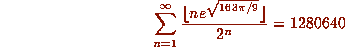
Sum 5 (correct to in excess of 42 billion digits)

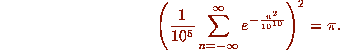
The Computational Component. Analysis of these and other
seemingly rational evaluations may be found in [6]. Sum 1 occured as a
problem proposed by Levine, College Math J., 19, #5,
(1989) and Bowman and White, MAA Monthly, 96 (1989),
745. Sum 2 relates to a problem of Diamond's in the MAA Monthly,
96 (1989), 838. Sums 2,3,4 all have transcendental values and are
explained by a lovely continued fraction expansion originally studied by
Mahler. Computer assisted analysis lead us to a similar more subtle
expansion for the generating function of 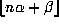 :
:


Sum 5 arises from an application of Poisson summation or equivalently as a modular transformation of a theta function. While asymptotically rapid, this series is initially very slow and virtually impossible for high-precision explicit computation.
These evaluations ask the question of how one develops appropriate intuition to be persuaded by say Sum 1 but not by Sum 2 or Sum 3? They also underline that no level of digit agreement is really conclusive of anything. Ten digits of coincidence is persuasive in some contexts while ten billion is misleading in others. In our experience, symbolic coincidence is much more impressive than undigested numeric coincidence.