![[Shownotes]](../gif/annotate/shide-51.gif)
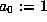 and
and 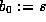 and define the cubic AGM by
and define the cubic AGM by

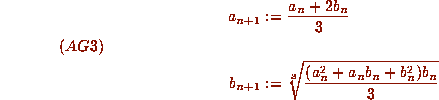 which converge cubically to a common limit
which converge cubically to a common limit

 where the hypergeometric function
where the hypergeometric function 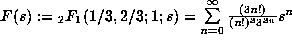 . In
particular, the hypergeometric function possesses the simple cubic
functional equation
. In
particular, the hypergeometric function possesses the simple cubic
functional equation 
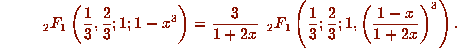 This can be validated
symbolically once known! As an example
This can be validated
symbolically once known! As an example 
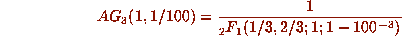 and 4 iterations of
and 4 iterations of  will compute the hypergeometric function at
will compute the hypergeometric function at
 to 25 significant digits. Any direct computation so near the
radius of convergence is doomed.
to 25 significant digits. Any direct computation so near the
radius of convergence is doomed.

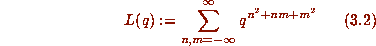 and
and 
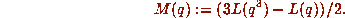
Theorem 2. The functions 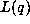 and
and 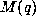 ``parametrize'' the
cubic AGM in the sense that if
``parametrize'' the
cubic AGM in the sense that if 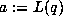 and
and 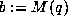 then
then

 and
and

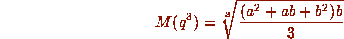 while
while 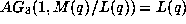 .
.
Thus a step of the iteration has the effect of sending q to 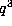 . From
this, one is led to an easy to state but hard to derive
. From
this, one is led to an easy to state but hard to derive
Cubic iteration for  . Let
. Let 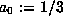 ,
, 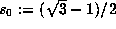 and set
and set

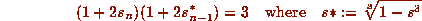

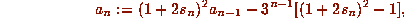 then
then 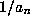 converges cubically to
converges cubically to  .
.
This iteration gives 1, 5,
21, 70,  digits correct and more than triples accuracy at each
step.
digits correct and more than triples accuracy at each
step.
The Computational Component. This is the most challenging and most satisfying of our three examples for computer assisted analysis. We began with one of Ramanujan's typically enigmatic entries in Chapter 20 of his notebook, now decoded in [1]. It told us that a ``quadratic modular equation'' relating to F was

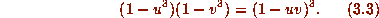 >From this we gleaned that some function R should exist so that
>From this we gleaned that some function R should exist so that 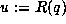 and
and 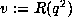 would solve
would solve 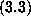 . We formally solved for the
coefficents of R and learned nothing. Motivated by the analogy with the
classical theory of the AGM iteration [2] we looked at
. We formally solved for the
coefficents of R and learned nothing. Motivated by the analogy with the
classical theory of the AGM iteration [2] we looked at 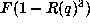 which
produced
which
produced


This was ``pay-dirt'' since the coefficients were sparse and very regular.
Some analysis suggested that they related to the number of representations
of the form 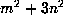 . From this we looked at theta function
representations and were rewarded immediately by the apparent identity
. From this we looked at theta function
representations and were rewarded immediately by the apparent identity
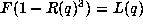 . Given the truth of this it was relatively easy to
determine that
. Given the truth of this it was relatively easy to
determine that 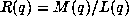 with M and L as in
with M and L as in 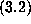 .
.
It was now clear that the behaviour as q goes to  should be at least
as interesting as
should be at least
as interesting as 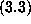 . Indeed, motivated by the modular properties of
L we observed symbolically that
. Indeed, motivated by the modular properties of
L we observed symbolically that

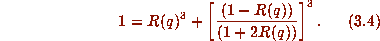
At this stage in [4] we resorted rather unsatisfactorily to a classical
modular function proof of 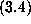 and so to a proof of Theorem 2. Later we
returned with Frank Garvan [8] to a search for an elementary proof. This
proved successful. By searching for product expansions for M we were lead
to an entirely natural computer-guided proof --- albeit with human insight
along the way.
and so to a proof of Theorem 2. Later we
returned with Frank Garvan [8] to a search for an elementary proof. This
proved successful. By searching for product expansions for M we were lead
to an entirely natural computer-guided proof --- albeit with human insight
along the way.
It is actually possible, as described in [8], to search for, discover and
prove  modular identities of the type of
modular identities of the type of 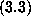 and
and 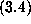 in an entirely automated fashion. Again, this is possible
because we have ultimately reduced most of the analytic questions to algebra
through the machinery of modular forms.
in an entirely automated fashion. Again, this is possible
because we have ultimately reduced most of the analytic questions to algebra
through the machinery of modular forms.
As a final symbolic challenge we observe that 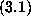 may be recast as
saying that
may be recast as
saying that

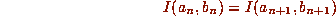 where
where

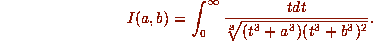 This invariance should be susceptible to a direct --- hopefully
experimentally guided --- proof.
This invariance should be susceptible to a direct --- hopefully
experimentally guided --- proof.