![[Shownotes]](../gif/annotate/shide-21.gif)
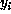 and
and 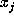 repectively. Define
repectively. Define
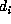 to be the distance between the dealer's secret card
to be the distance between the dealer's secret card 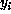 and the
player's next closest secret card into the deck. Clearly
and the
player's next closest secret card into the deck. Clearly
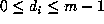 ,
and we define the states of our Markov process to be these m
distances. The absorbing state is the distance 0 (For a good treatment
of Markov Processes, see [1]).
,
and we define the states of our Markov process to be these m
distances. The absorbing state is the distance 0 (For a good treatment
of Markov Processes, see [1]).
Let 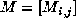 be the transition matrix. If m is the
number of states (i.e. face cards) we let
be the transition matrix. If m is the
number of states (i.e. face cards) we let
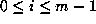 and
and 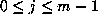 denote the index entries
of M, in contrast with the standard convention. This enumeration
of M's entries is more natural for us because it clarifies the fact
that
denote the index entries
of M, in contrast with the standard convention. This enumeration
of M's entries is more natural for us because it clarifies the fact
that 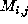 is the probability that if for some k
the distance
is the probability that if for some k
the distance 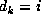 , then
, then 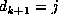 .
.
For all 0 < i < m-1, we have
The closed form of the transition matrix M now follows easily.
(d) The initial vector I is given by
The characteristic polynomial of M is
