|
Project Leaders:
Dr. George Labahn (University of Waterloo) and
Dr. Michael Monagan (Simon Fraser University)
Our 2006 MITACS project proposal (.pdf)
Our 2008 MITACS project proposal (.pdf)
Our 2010 MITACS short project proposal (.pdf)
The Computer Algebra community in Canada is strong, coherent and cohesive, and
clearly lends itself to functioning as a consortium. It has three substantial nodes at
the University of Waterloo, the University of Western Ontario and Simon Fraser
University. Each has a core of engaged scientists and students. As well, there is significant
ancillary expertise, notably at the University of Calgary, McMaster University, and
UQAM. It is not possible to promote, unify and fund this group as a single MITACS
project, hence the existence of the Consortium.
The features that drive the success of the consortium are:
- the size, intellectual strength and breadth of the consortium
- the focus and cohesiveness of the consortium community
- the importance to the mathematical sciences of the problems
- the scientific track record
- the management track record
- the track record in training of Highly Qualified Personnel
- the track record of interaction with industry
The project addresses central problems in algebraic computation. This means developing and
implementing algorithms for finding the exact solution(s) to mathematical problems. For example, we
may prefer the output 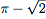 to the output 1.727379092. We may prefer the output to the output 1.727379092. We may prefer the output 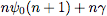 to
the "unknown" sequence of numbers 1, 3, 11/2, 25/3, 137/12, 147/10,.... Or we may be interested in the
asymptotics of a solution, e.g. to
the "unknown" sequence of numbers 1, 3, 11/2, 25/3, 137/12, 147/10,.... Or we may be interested in the
asymptotics of a solution, e.g. 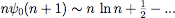
Because exact formulae tend to grow in size rapidly, algorithmic efficiency and the ability to simplify
formulae, that is, to find a compact representation for a formula, is one problem we address. Another
problem is that some algorithms require tools from analysis. Our goal here is to be able to deal with
analytic concepts in a computational setting (specifically in Maple) as easily as one can already do
with algebraic concepts. The scope of the research program includes problems like exact definite
integration and summation, finding analytical solutions of ordinary differential equations, solving systems
of algebraic and/or differential equations (both ODEs and PDEs), identity and inequality verification, and
simplification of algebraic formulae involving symbols representing vectors and matrices as well as
integers and reals.
As well as this fundamental research, our program aims to make the results accessible and visible to a
wider community by incorporating procedures into Maple and through the production of interactive
mathematical tools accessible from the internet.
|





