|
Fraction-Free Computation of Simulataneous Pade Approximants.
|
Bernhard Beckermann and George Labahn.
Proceedings of ISSAC 2009, ACM Press, pp. 15-22, July 2009.
Abstract:
In this paper we give a new, fast algorithm for solving the simulataneous
Pade approximation problem. The algorithm is fraction-free and is suitable
for computation in domains where growth of coefficients in intermediate
computations is a central concern. The algorithm gives significant
improvement on previous fraction-free methods, in particular when solved
via the use of vector Hermite-Pade approximations using the FFG order basis
algorithm previously done by the authors. The improvements are both
in terms of bit complexity and in reduced size of intermediate quantities.
|
Triangular Decomposition of Semi-Algebraic Sets.
|
Changbo Chen, James H. Davenport, John P. May,
Marc Moreno Maza, Bican Xia, Rong Xiao.
Proceedings of ISSAC '2010, ACM Press, pp. 187-194, 2010.
Abstract:
Regular chains and triangular decompositions are fundamental
and well developed tools for describing the complex solutions of
polynomial systems. This paper proposes adaptions of these tools
focusing on solutions of the real analogue: semi-algebraic systems.
We show that any such system can be decomposed into finitely many
regular semi-algebraic systems. We propose two specifications
of such a decomposition and present corresponding algorithms. Under
some assumptions, one type of decomposition can be computed in singly
exponential time w.r.t. the number of variables. We implement our
algorithms and the experimental results illustrate their effectiveness.
|
Detecting lacunary perfect powers and computing their roots.
|
Mark Giesbrecht and Daniel Roche.
To appear in Journal of Symbolic Computation, 21 pages, 2010.
Abstract:
We consider the problem of determining whether a lacunary (also called a
super-sparse) polynomial f is a perfect power, that is,
f = hr for some polynomial h and r ∈ N,
and of finding h and r should
they exist. We show how to determine if f is a perfect power
in time polynomial in the number of non-zero terms of f, and in terms
of log deg f, i.e., polynomial in the size of the lacunary representation.
The algorithm works over Fq[x] (for large
characteristic)) and over Z[x], where the cost is also polynomial
in log ||f||∞. We also give a Monte Carlo algorithm
to find h if it exists, for which our proposed algorithm requires
polynomial time in the output size, i.e., the sparsity and height of h.
Conjectures of Erdös and Schinzel, and recent work of Zannier, suggest
that h must be sparse. Subject to a slightly stronger conjecture we
give an extremely efficient algorithm to find h via a form of sparse
Newton interpolation. We demonstrate the efficiency of these algorithms
with an implementation using the C++ library NTL.
|
Distance-Based Classification of Handwritten Symbols.
|
Oleg Golubitsky and Stephen M. Watt
Int. J. of Document Analysis and Recognition, 13:2, 133-146, 2010
Abstract:
We study online classification of isolated handwritten symbols using
distance measures on spaces of curves. We compare three distance-based measures
on a vector space representation of curves to elastic matching and ensembles
of SVM. We consider the Euclidean and Manhattan distances and the distance
to the convex hull of nearest neighbors. We show experimentally that of
all these methods the distance to the convex hull of nearest neighbors yields the
best classification accuracy of about 97.5%. Any of the above distance measures
can be used to find the nearest neighbors and prune totally irrelevant classes,
but the Manhattan distance is preferable for this because it admits a very efficient
implementation. We use the first few Legendre-Sobolev coefficients of the
coordinate functions to represent the symbol curves in a finite-dimensional vector
space and choose the optimal dimension and number of bits per coefficient
by cross-validation. We discuss an implementation of the proposed classification
scheme that will allow classification of a sample among hundreds of classes in a
setting with strict time and storage limitations.
|
Parallel Sparse Polynomial Interpolation over Finite Fields.
|
Mahdi Javadi and Michael Monagan.
Proceedings of PASCO '2010, ACM Press, pp. 160-168, July 2010.
Abstract:
We present a probabilistic algorithm to interpolate a sparse
multivariate polynomial over a finite field, represented with a black box.
Our algorithm modifies the algorithm of Ben-Or and Tiwari from 1988 for
interpolating polynomials over rings with characteristic zero to
characteristic p by doing additional probes.
To interpolate a polynomial in n variables with t non-zero terms,
Zippel's (1990) algorithm interpolates one variable at a time
using O(ndt) probes to the black box where d bounds the degree
of the polynomial. Our new algorithm does O(nt) probes.
It interpolates each variable independently using O(t) probes
which allows us to parallelize the main loop giving an advantage over
Zippel's algorithm.
We have implemented both Zippel's algorithm and the new algorithm in C
and we have done a parallel implementation of our algorithm using Cilk.
In the paper we provide benchmarks comparing the number of probes
our algorithm does with both Zippel's algorithm and Kaltofen and
Lee's hybrid of the Zippel and Ben-Or/Tiwari algorithms.
|
Advances in the Theory of Box Integrals.
|
D. H. Bailey, J. M. Borwein and R. E. Crandall.
Mathematics of Computation, 79:271, 1839-1866, July 2010.
Abstract:
Box integrals
— expectations <|rs|> or
<|rs-qs|> over the unit n-cube
—
have over the decades been occasionally given closed forms for isolated
n, s. By employing experimental mathematics together with a new,
global analytic strategy, we prove that for each n = 1,2,3,4 dimensions
the obx integrals are for any integer s hypergeometrically closed
("hyperclosed") in an explicit sense we clarify herein. For n = 5
dimensions, susch a complete closure proof is blocked by a single,
unresolved integral we call K5; although we do prove
that all but a finite set of (n = 5) cases enjoy hyperclosure.
We supply a compendium of exemplary closed forms that arise naturally
from the theory.
|
Fast arithmetics in Artin-Schreier towers over finite fields.
|
L. De Feo and É. Schost.
Proceedings of ISSAC '09, pp. 127-134, ACM Press, 2009.
Distinguished Student Paper Award at ISSAC '09.
Abstract:
An Artin-Schreier tower over the finite field Fp
is a tower of field extensions generated by polynomials of the form
Xp-X-α. Following Cantor and Couveignes,
we give algorithms with quasi-linear time complexity for arithmetic
operations in such towers. As an application, we present an implementation
of Couveignes' algorithm for computing isogenies between elliptic curves
using the p-torsion.
|
Efficient Computation of Order Bases.
|
G. Labahn and W. Zhou..
Proceedings of ISSAC '09, pp. 375-382, ACM Press, 2009.
Abstract:
In this paper we give an efficient algorithm for computation of order basis of a matrix of power series. For a problem with an m x n input matrix over a field K, m ≤ n, and order σ, our algorithm uses O(MM(n, ⊂O~(nω⌈mσ/n⌉) field operations in B.K, where the soft-O notation O~ is Big O with log factors omitted and MM(n,d) denotes the cost of multiplying two polynomial matrices with dimension n and degree d. The algorithm extends earlier work of Storjohann, whose method can be used to find a subset of an order basis that is within a specified degree bound δ using O~(MM(n,δ)) field operations for δ≥⌈ mσ/n⌉.
|
Parallel Sparse Polynomial Multiplication using Heaps
|
M. Monagan and R. Pearce.
Proceedings of ISSAC '09, pp. 263-269, ACM Press, 2009.
Abstract:
We present a high performance algorithm for multiplying sparse distributed
polynomials using a multicore processor.
Each core uses a heap of pointers to multiply parts of the polynomials using its local cache.
Intermediate results are written to buffers in shared cache and the cores take
turns combining them to form the result.
A cooperative approach is used to balance the load and improve scalability,
and the extra cache from each core produces a superlinear speedup in practice.
We present benchmarks comparing our parallel routine to a sequential version
and to the routines of other computer algebra systems.
|
Balanced Dense Polynomial Multiplication on Multi-cores.
|
M. Moreno Maza and Y. Xie.
Proceedings of PDCAT '09, 9 pages, IEEE Press, 2009.
Best Poster Award at ISSAC '09.
Abstract:
In symbolic computation, polynomial multiplication
is a fundamental operation
akin to matrix multiplication in numerical computation.
We present efficient implementation strategies for FFT-based
dense polynomial multiplication targeting multi-cores.
We show that balanced input data can maximize
parallel speedup and minimize cache complexity
for bivariate multiplication.
However, unbalanced input data, which are common in symbolic
computation, are challenging.
We provide efficient techniques, that we call
contraction and extension,
to reduce
multivariate (and univariate) multiplication to
balanced bivariate multiplication.
Our implementation in Cilk++ demonstrates good speedup
on multi-cores.
|
High Precision Numerical Integration: Progress and Challenges.
|
David Bailey and Jonathan Borwein.
To appear, Journal of Symbolic Computation, 19 pages, 2009.
Abstract:
One of the most fruitful advances in the field of experimental mathematics
has been the development of practical methods for very high-precision numerical
integration, a quest initiated by Keith Geddes and other researchers in the
1980s and 1990s. These techniques, when coupled with equally powerful
integer relation detection methods, have resulted in the analytic evaluation
of many integrals that previously were beyond the realm of symbolic techniques.
This paper presents a survey of the current state-of-the-art in this area
(including results by the present authors), mentions some new results,
and then sketches what challenges lie ahead.
|
2007-2008
Fast arithmetic for triangular sets: from theory to practice.
|
Xin Li, Marc Moreno Maza and Eric Schost.
Journal of Symbolic Computation, in press, November 2008.
Abstract:
We study arithmetic operations for triangular families of polynomials,
concentrating on multiplication in dimension zero. By a suitable extension
of fast univariate Euclidean division, we obtain theoretical and practical
improvements over a direct recursive approach; for a family of special
cases, we reach quasi-linear complexity. The main outcome we have in mind
is the acceleration of higher-level algorithms, by interfacing our low-level
implementation with languages such as AXIOM or Maple. We show the potential
for huge speed-ups, by comparing two AXIOM implementations of van Hoeij and
Monagan's modular GCD algorithm.
|
Faster Algorithms for the Characteristic Polynomial
|
C. Pernet and A. Storjohann.
Proceedings of ISSAC '07, ACM Press, pp. 307-314, 2008
Abstract:
A new randomized algorithm is presented for computing the characteristic
polynomial of an n by n matrix over a field. Over a sufficiently large
field the asymptotic complexity of the algorithm is O(n^w) field operations,
improving, by a factor of log n on the worst case complexity of
Keller-Gehrig's algorithm.
|
Sparse Polynomial Division using a Heap.
|
M. Monagan and R. Pearce.
Submitted September 2008 to Journal of Symbolic Computation.
Abstract:
In 1974 Johnson showed how to multiply and divide sparse polynomials using a binary heap.
This paper introduces a new algorithm that uses a heap to divide with the same
complexity as multiplication. It is a fraction-free method that reduces integer
arithmetic for divisions over Q by up to an order of magnitude.
The heap algorithms use very little memory and generate no garbage.
They can run in the cpu cache and achieve high performance.
We also present benchmarks comparing our implementation
of sparse polynomial multiplication and division in C
to existing computer algebra systems.
|
Elliptic integral representation of Bessel moments.
|
David H. Bailey, Jonathan M. Borwein, David Broadhurst and M.L. Glasser.
J. Phys. A: Math. Theory, 41 (2008), 5203-5231.
Abstract:
We record and substantially extend what is known about the closed forms for
various Bessel function moments arising in quantum field theory, condensed
matter theory and other parts of mathematical physics. In particular, we
develop formulae for integrals of products of six or fewer Bessel functions.
In consequence, we are to able to discover and prove closed forms for
$c_{n,k} := int_0^{\infty} t^k K_0^n(t) dt$ with integers $n=1,2,3,4$ and $k \ge 0$
obtaining new results for even moments $c_{3,2k}$ and $c_{4,2k}$.
We also derive new closed forms for the odd moments
$s_{n,2k+1} := \int_0^{\infty} t^{2k+1} I_0^2(t) K_0^{n-2}(t) dt$ with $n=5$
relating the latter to Green functions on hexagonal, diamond and cubic lattices.
We conjecture the values of $s_{5,2k+1}$, make substantial progress on the
evaluation of $c_{5,2k+1}, s_{6,2k+1}$ and $t_{6,2k+1}$ and report more limited
progress regarding $c_{5,2k}, c_{6,2k+1}$ and $c_{6,2k}$. In the process,
we obtain eight conjectural evaluations, each of which has been
checked to 1200 decimal places. One of these lies deep in four-dimensional
quantum field theory and two are probably provable by delicate combinatorics.
There remains a hard core of five conjectures whose proofs would be most
instructive, to mathematicians and physicists alike.
|
Symbolic-numeric Sparse Interpolation of Multivariate Polynomials
|
Mark Giesbrecht, George Labahn and Wen-shin Lee.
Proceedings of Computer Algebra in Scientific Computing (CASC '07),
To appear in J. Symb. Comput.
Abstract:
We consider the problem of sparse interpolation of an approximate multivariate black-box polynomial in
foating-point arithmetic. That is, both the inputs and outputs of the black-box
polynomial have some error, and all numbers are represented in standard, fixed-precision,
foating- point arithmetic. By interpolating the black box evaluated at random primitive roots of unity,
we give efficient and numerically robust solutions. We note the similarity between
the exact Ben-Or/Tiwari sparse interpolation algorithm and the classical Prony's method
for interpolating a sum of exponential functions, and exploit the generalized eigenvalue
reformulation of Prony's method. We analyze the numerical stability of our algorithms and
the sensitivity of the solutions, as well as the expected conditioning achieved through
randomization. Finally, we demonstrate the effectiveness of our techniques in practice
through numerical experiments and applications.
|
2005-2006
Barker Sequences and Flat Polynomials.
|
P. Borwein and M. Mossingoff.
Proceedings of Number Theory and Polynomials Conference,
Bristol, 3-7 April 2006. Accepted January 2007.
Abstract:
A Barker sequence is a finite sequence of integers, each +1 or -1, whose
aperiodic autocorrelations are all as small as possible. It is widely conjectured
that only finitely many Barker sequences exist. We describe connections between
Barker sequences and several problems in analysis regarding the existence of
polynomials with +1, -1 coefficients that remain flat over the unit circle according
to some criterion. First, we amend an argument of Saffari to show that a polynomial
constructed from a Barker sequence remains within a constant factor of its L2 norm
over the unit circle, in connection with a problem of Littlewood. Second, we show
that a Barker sequence produces a polynomial with very large Mahler's measure,
in connection with a question of Mahler. Third, we optimize an argument of Newman
to prove that any polynomial with +1, -1 coefficients and positive degree n-1 has L1
norm less than sqrt(n-0.09) and note that a slightly stronger statement would
imply that long Barker sequences do not exist. We also record polynomials with
+1, -1 coefficients having maximal L1 norm or maximal Mahler's measure for each
fixed degree up to 24. Finally, we show that if one could establish that the
polynomials in a particular sequence are all irreducible over Q, then an
alternative proof that there are no long Barker sequences with odd length would follow.
|
Solving Sparse Rational Linear Systems.
|
W. Eberly, M. Giesbrecht, P. Giorgi, A. Storjohann, G. Villard.
Proceedings of ISSAC '06, 63-70. ACM Press, 2006.
Abstract:
We propose a new algorithm to find a rational solution to a sparse
system of linear equations over the integers. This algorithm is
based on a p-adic lifting technique combined with
the use of block matrices with structured blocks. It achieves
a sub-cubic complexity in terms of machine operations subject
to a conjecture on the effectiveness of certain sparse projections.
A LINBOX-based implementation of this algorithm is demonstrated,
and emphasizes the practical benefits of this new method over the
previous state of the art.
|
Symbolic-numeric Sparse Interpolation of Multivariate Polynomials.
|
Mark Giesbrecht, George Labahn and Wen-shin Lee.
Proceedings of ISSAC '06, 116-123. ACM Press, 2006.
Abstract:
We consider the problem of sparse interpolation of an approximate
multivariate black-box polynomial in floating-point arithmetic.
That is, both the inputs and outputs of the black-box polynomial
have some error, and all numbers are represented in standard
fixed-precision, floating point arithmetic. By interpolating the
black box at random roots of unity, we give efficient
and numerically robust solutions. We note the similarity between
the exact Ben-Or/Tiwari sparse interpolation algorithm and the
classical Prony's method for interpolating a sum of exponential
functions, and exploit the generalized eigenvalue reformulation
of Prony's method. We analyze the numerical stability of our
algorithms and the sensitivity of the solutions, as well as the
expected conditioning achieved through randomization.
Finally, we demonstrate the effectiveness of our techniques
in practice through numerical experiments and applications.
|
Normal forms for General Polynomial Matrices.
|
B. Beckermann, George Labahn and Gilles Villard.
Journal of Symbolic Computation 41(6) (2006) 708-737.
Abstract:
We present an algorithm for the computation of a shifted
Popov Normal Form of a rectangular polynomial matrix.
For specific shifts, we obtain methods for computing the
matrix greatest common divisor of two matrix polynomials
(in normal form) or such polynomial normal form computation
as the classical Popov form and the Hermite Normal Form.
The method is done by embedding the problem of computing shifted
forms into one of computing matrix rational approximants. This
has the advantage of allowing for fraction-free computations
over integral domains such as Z[z] or
K[a1, ..., an][z].
In the case of rectangular matrix input, the corresponding
multipliers for shifted forms are not unique. We use the
concept of minimal matrix approximants to introduce a
notion of minimal multipliers and show how such
multipliers are computed by our methods.
|
Lifting Techniques for Triangular Decompositions.
|
X. Dahan, M. Moreno-Maza, E. Schost, W. Wu and Y. Xie.
Proceedings of ISSAC 2005, Beijing China, ACM Press, (2005) 108-115.
Abstract:
We present lifting techniques for triangular decompositions of zero-dimensional
varieties that extend the range of previous methods We discuss complexity
aspects, and report on a preliminary implementation. Our theoretical results
are comforted by these experiments.
|
Rational Simplification Modulo a Polynomial Ideal.
|
R. Pearce and M. Monagan
Proceedings of ISSAC 2006, Genoa, Italy, ACM Press, (2006) 239-245.
Abstract:
We present two algorithms for simplifying rational
expressions modulo an ideal of the polynomial ring k[x1,...,xn].
The first method generates the set of equivalent expressions as a
module over k[x1,...,xn] and computes a reduced Groebner basis.
From this we obtain a canonical form for the expression up to our choice
of monomial order for the ideal.
The second method constructs equivalent expressions by solving systems of linear equations
over k, and conducts a global search for an expression with minimal total degree.
Depending on the ideal, the algorithms may or may not cancel all common divisors.
We also provide some timings comparing the efficiency of the algorithms in Maple.
|
2003-2004
Telescoping in the context of symbolic summation in Maple.
|
S.A. Abramov, J.J. Carette, K.O. Geddes, and H.Q. Le.
Journal of Symbolic Computation, 38 (4), Oct 2004, pp. 1303-1326.
Abstract:
This paper is an exposition of different methods for computing closed forms of
definite sums. The focus is on recently-developed results on computing closed
forms of definite sums of hypergeometric terms. A design and an implementation
of a software package which incorporates these methods into the computer algebra
system Maple are described in detail.
|
Zeros of partial sums of the Riemann zeta-function.
|
P. Borwein, G. Fee, R. Ferguson and A. van der Waall
Accepted, Journal of Experimental Mathematics, August 2005.
|
Reasoning about the elementary functions of complex analysis.
|
R.M. Corless, D.J. Jeffrey, S.M. Watt, R. Bradford, J.H. Davenport
Annals of Mathematics and Artificial Intelligence, 36 (3), Nov 2002, pp. 303-18. Abstract:
There are many problems with the simplification of elementary functions, particularly
over the complex plane, though not exclusively. Systems tend to make
"howlers" or not to simplify enough. In this paper we outline the "unwinding number"
approach to such problems, and show how it can be used to prevent errors and to
systematise such simplification, even though we have not yet reduced the
simplification process to a complete algorithm. The unsolved problems are probably
more amenable to the techniques of artificial intelligence and theorem proving than
the original problem of complex-variable analysis.
|
Factoring and Decomposing Ore Polynomials over Fq(t).
Algorithms for Polynomial GCD Computation over Algebraic Function Fields.
|
M. van Hoeij, M. B. Monagan
Proceedings of ISSAC '2004, ACM Press, pp. 297-304, 2004.
Abstract:
Let L be an algebraic function field in k ≥ 0 parameters
t1, ... , tk. Let f1,
f2 be non-zero polynomials in L[x]. We
give two algorithms for computing their gcd. The first, a modular GCD algorithm,
is an extension of the modular GCD algorithm of Brown for
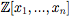 and Encarnacion for and Encarnacion for 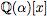 to function fields. The second, a fraction-free algorithm, is a modification
of the Moreno Maza and Rioboo algorithm for computing gcds over triangular sets.
The modification reduces coefficient growth in L to be linear. We give
an empirical comparison of the two algorithms using implementations in Maple.
to function fields. The second, a fraction-free algorithm, is a modification
of the Moreno Maza and Rioboo algorithm for computing gcds over triangular sets.
The modification reduces coefficient growth in L to be linear. We give
an empirical comparison of the two algorithms using implementations in Maple.
|
|





