![[Shownotes]](../gif/annotate/shide-81.gif)
I asked Doron Zeilberger to comment on the observations within Section
5, and the following is a very slightly edited version of his
response:
``The method of creative telescoping of [15] boils down to solving a
homogeneous system of linear equations with symbolic
coefficients. When there are extra parameters as in Section 5 (x
and z, in addition to m), the matrix of coefficients contains
polynomials of the three variables 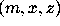 . It is very time and
memory consuming to solve such a huge system with symbolic
coefficients.
. It is very time and
memory consuming to solve such a huge system with symbolic
coefficients.
``Because it is very fast to solve the system with specific values assigned to m, x, and z, and the solutions are rational functions of x,z,m, it should be possible (and most likely this has been done for other programming languages) to solve the system for sufficiently many special cases, and then combine them by `interpolation' (using, for example the Fast Fourier Transform). This can also be easily parallelized, so the inability of the WZ method to do (5.5) is far from getting close to the borderline of real-time computational feasibility. ``This still doesn't explain the `slack' in the order of the recurrence. (5.5) obviously satisfies a first order recurrence, but the method of creative telescoping yields 3 orders too many, i.e. order=4. A similar situation occurred with Ekhad and Tre's proof of Andrews's finite form of Rogers-Ramanujan.
``Very recently Peter Paule showed how a slight change in the presentation of the data (taking advantage of the symmetry of the summand) gives a much shorter WZ proof, with the minimal recurrence. He also gave many other examples, all with q-series however.
``Probably a similar situation is responsible for the difficulty of the WZ-proof of (5.5). Unfortunately so far the right symmetry has not been found.''
In addition, Herb Wilf has noted that Marko Petkovsek has developed
an algorithm for checking whether a given WZ recurrence might indeed
reduce to one of lower order. Thus the combination of this algorithm
with the WZ method would produce a first order recurrence for (5.5)
once the fourth order recurrence had been determined via WZ. This
algorithm would immediately reduce the second order recurrence (3.2)
to the desired first order recurrence.