



Contents
Next: Applications of the
Up: No Title
Previous: Introduction
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-31.gif)
2. The PSLQ Integer Relation Algorithm
In 1991 a new algorithm, known as ``PSLQ'' algorithm, was developed by
Ferguson [12]. It appears to combine some of the best features
separately possessed by previous algorithms, including fast run times,
numerical stability, numerical efficiency (i.e. successfully
recovering a relation when the input is known to only limited
precision), and a guaranteed completion in a polynomially bounded
number of iterations. More recently a much simpler formulation of
this algorithm was developed, and it has been extended to the complex
number field
[13]. This newer, simpler version of PSLQ can be stated as
follows:
Let x be the n-long input real vector, and let nint denote the
nearest integer function (for exact half-integer values, define nint
to be the integer with greater absolute value). Let 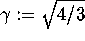 . Then perform the following:
. Then perform the following:
Initialize:
- Set the
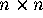 matrices A and B to the identity.
matrices A and B to the identity.
- For
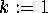 to n: compute
to n: compute 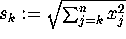 ;
endfor. For
;
endfor. For 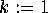 to n:
to n: 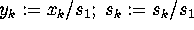 ;
endfor.
;
endfor.
- Compute the
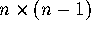 matrix H as follows:
matrix H as follows:
For 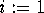 to n: for
to n: for 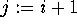 to n - 1: set
to n - 1: set 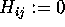 ;
endfor; if
;
endfor; if 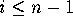 then set
then set 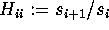 ; for
; for 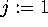 to i - 1: set
to i - 1: set 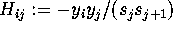 ; endfor;
endfor.
; endfor;
endfor.
- Perform full reduction on H, simultaneously updating
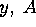 and B:
and B:
For 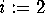 to n: for
to n: for 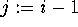 to 1 step -1:
to 1 step -1: 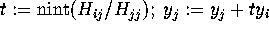 ; for
; for 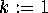 to j:
to j:
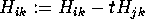 ; endfor; for
; endfor; for 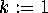 to n:
to n: 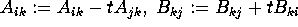 ; endfor;
endfor; endfor.
; endfor;
endfor; endfor.
Repeat until precision is exhausted or a relation has been detected:
- Select m such that
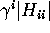 is maximal when i = m.
is maximal when i = m.
- Exchange entries m and m + 1 of y, corresponding rows of
A and H, and corresponding columns of B.
- If
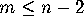 then update H as follows:
then update H as follows:
Set 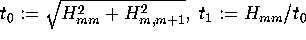 and
and 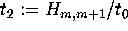 . Then for
. Then for 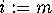 to n:
to n: 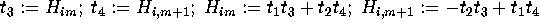 ; endfor.
; endfor.
- Perform block reduction on H, simultaneously updating
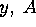 and B:
and B:
For 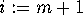 to n: for
to n: for 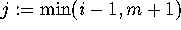 to 1 step
-1:
to 1 step
-1: 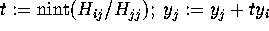 ;
for
;
for 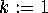 to j:
to j: 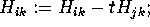 ; endfor;
for
; endfor;
for 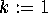 to n:
to n: 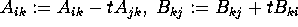 ; endfor; endfor; endfor.
; endfor; endfor; endfor.
- Norm bound: Compute
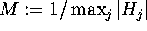 , where
, where 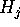 denotes
the j-th row of H. Then there can exist no relation vector whose
Euclidean norm is less than M.
denotes
the j-th row of H. Then there can exist no relation vector whose
Euclidean norm is less than M.
- Termination test: If the largest entry of A exceeds the level
of numeric precision used, then precision is exhausted. If the
smallest entry of the y vector is less than the detection threshold,
a relation has been detected and is given in the corresponding column
of B.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-32.gif)
With regards to the termination criteria in step 6, it sometimes
happens that a relation is missed at the point of potential detection
because the y entry is not quite as small as the detection threshold
being used (the threshold is typically set to the ``epsilon'' of the
precision level). When this happens, however, one will note that the
ratio of the smallest and largest y vector entries is suddenly very
small, provided sufficient numeric precision is being used. In a
normal computer run using the PSLQ algorithm, prior to the detection
of a relation, this ratio is seldom smaller than 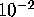 . Thus if
this ratio suddenly decreases to a very small value, such as
. Thus if
this ratio suddenly decreases to a very small value, such as
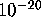 , then almost certainly a relation has been detected --- one
need only adjust the detection threshold for the algorithm to
terminate properly and output the relation. When detection does
occur, this ratio may be thought of as a ``confidence level'' of the
detection.
, then almost certainly a relation has been detected --- one
need only adjust the detection threshold for the algorithm to
terminate properly and output the relation. When detection does
occur, this ratio may be thought of as a ``confidence level'' of the
detection.
![[Annotate]](/organics/icons/sannotate.gif)
![[Shownotes]](../gif/annotate/shide-33.gif)
As a general rule, one can expect to detect a relation of degree n,
with coefficients of size 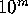 , provided that the input vector is
known to somewhat greater than m n digit precision, and provided
that computations are performed using at least this level of numeric
precision.
, provided that the input vector is
known to somewhat greater than m n digit precision, and provided
that computations are performed using at least this level of numeric
precision.


Contents
Next: Applications of the
Up: No Title
Previous: Introduction
![[Shownotes]](../gif/annotate/shide-31.gif)
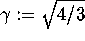 . Then perform the following:
. Then perform the following:
 matrices A and B to the identity.
matrices A and B to the identity.
 to n: compute
to n: compute 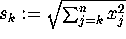 ;
endfor. For
;
endfor. For 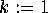 to n:
to n: 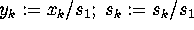 ;
endfor.
;
endfor.
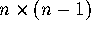 matrix H as follows:
matrix H as follows:
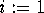 to n: for
to n: for 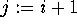 to n - 1: set
to n - 1: set 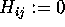 ;
endfor; if
;
endfor; if 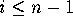 then set
then set 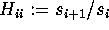 ; for
; for 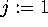 to i - 1: set
to i - 1: set 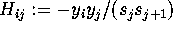 ; endfor;
endfor.
; endfor;
endfor.
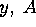 and B:
and B:
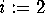 to n: for
to n: for 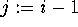 to 1 step -1:
to 1 step -1: 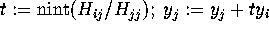 ; for
; for 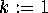 to j:
to j:
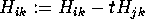 ; endfor; for
; endfor; for 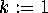 to n:
to n: 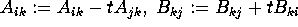 ; endfor;
endfor; endfor.
; endfor;
endfor; endfor.
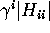 is maximal when i = m.
is maximal when i = m.
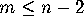 then update H as follows:
then update H as follows:
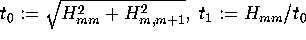 and
and 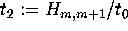 . Then for
. Then for 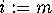 to n:
to n: 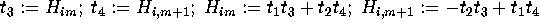 ; endfor.
; endfor.
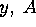 and B:
and B:
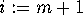 to n: for
to n: for 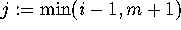 to 1 step
-1:
to 1 step
-1: 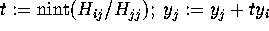 ;
for
;
for 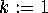 to j:
to j: 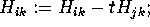 ; endfor;
for
; endfor;
for 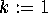 to n:
to n: 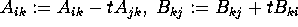 ; endfor; endfor; endfor.
; endfor; endfor; endfor.
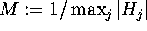 , where
, where 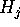 denotes
the j-th row of H. Then there can exist no relation vector whose
Euclidean norm is less than M.
denotes
the j-th row of H. Then there can exist no relation vector whose
Euclidean norm is less than M.
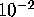 . Thus if
this ratio suddenly decreases to a very small value, such as
. Thus if
this ratio suddenly decreases to a very small value, such as
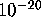 , then almost certainly a relation has been detected --- one
need only adjust the detection threshold for the algorithm to
terminate properly and output the relation. When detection does
occur, this ratio may be thought of as a ``confidence level'' of the
detection.
, then almost certainly a relation has been detected --- one
need only adjust the detection threshold for the algorithm to
terminate properly and output the relation. When detection does
occur, this ratio may be thought of as a ``confidence level'' of the
detection.
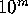 , provided that the input vector is
known to somewhat greater than m n digit precision, and provided
that computations are performed using at least this level of numeric
precision.
, provided that the input vector is
known to somewhat greater than m n digit precision, and provided
that computations are performed using at least this level of numeric
precision.