![[Shownotes]](../gif/annotate/shide-71.gif)
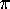 , as well as a number of other constants.
A brief review of these results is as follows. First, let us ask
whether
, as well as a number of other constants.
A brief review of these results is as follows. First, let us ask
whether 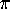 satisfy a relation of the form
satisfy a relation of the form

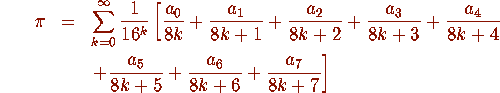
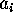 are rational numbers? Indeed it does. Such a formula can
be found by separating the right hand side of the above expression
into eight summations, numerically evaluating these to high precision,
appending the numerical value of
are rational numbers? Indeed it does. Such a formula can
be found by separating the right hand side of the above expression
into eight summations, numerically evaluating these to high precision,
appending the numerical value of 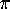 , and applying PSLQ to the
resulting 9-long vector. When this is done, PSLQ discovers the
following formula:
, and applying PSLQ to the
resulting 9-long vector. When this is done, PSLQ discovers the
following formula:

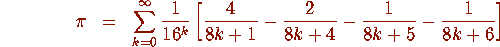
The significance of these formulas for the computation of 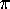 can be
seen as follows. Let
can be
seen as follows. Let 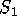 be the first of the sums in the above
formula for
be the first of the sums in the above
formula for 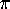 . Then we can write
. Then we can write

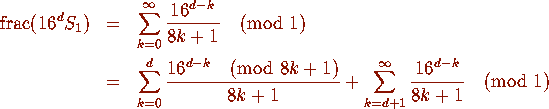
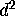 . Once an
individual exponentiation operation is complete, the resulting integer
value is divided by 8 k + 1, using floating-point arithmetic, and
added to the sum modulo 1. Only a few terms are required of the
second, since the terms rapidly become smaller than the ``machine
epsilon'' of the floating-point arithmetic system being used. The
resulting fractional value, when expressed in base 16 notation, gives
the hexadecimal digits of
. Once an
individual exponentiation operation is complete, the resulting integer
value is divided by 8 k + 1, using floating-point arithmetic, and
added to the sum modulo 1. Only a few terms are required of the
second, since the terms rapidly become smaller than the ``machine
epsilon'' of the floating-point arithmetic system being used. The
resulting fractional value, when expressed in base 16 notation, gives
the hexadecimal digits of 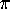 beginning at position d + 1.
beginning at position d + 1.

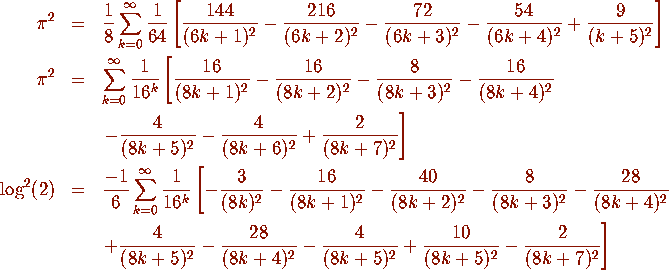
Full details of these calculations, as well as formal proofs of the
above formulas, can be found in [5].